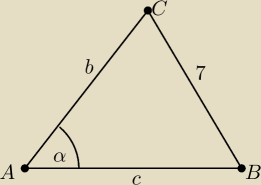
Trójkąt i iloczyn skalarny Mi Ka: W trójkącie ABC mamy dane AB^→AC^→=20 AB+AC=13 Oblicz AB i AC oraz miarę kąta BAC AB^→*AC^→=20 BC=7 |AB|=c |AC|=b b+c=13 c=13−b ∡|BAC|=α Obliczyć AB i AC oraz miarę kąta BAC AB^→*AC^→=|AB|*|AC|*cos∡|BAC|=c*b*cosα=20 Z twierdzenia cosinusów 7²=(13−b)²+b²−2*c*b*cosα 49=169−26b+2b²−40 −80=2b²−26b −2b²+26b−80=0 2b²−26b+80=0 Δ=(−26)²−4*160=676−640=36

	26−6
b1=		=5
	4

AC₁=5 to |AB|=c=8

	26+6
b2=		=8
	4

AC₂=8 to |AB|=c=5 Dla b=5 i c=8 i tak samo będzie dla b=8 i c=5 b*c*cosα=20

	1		π
5*8*cosα=20 cosα=		α=
	2		3