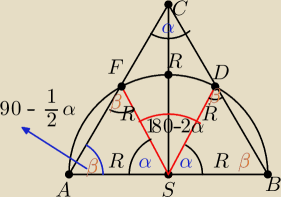
trójkat Mi Ka: Podstawa AB trójkąta równoramiennego ABC jest średnica okręgu o danym promieniu R Kąt C jest ostry i równa się α. Obliczyc pole powierzchni tej części trójkąta która leży na zewnątrz okręgu α<90^o |AS|=SB|=|FS|=|SD|=R Obliczyc P_FRDC P_FRDC=P_ABC−2P{AFS}−P_FSDR

	1
PABC=		|AB|*|SC|
	2

W trójkącie ASC

|SC|		1
	=tg(90o−		α)
|AS|		2

|SC|		1
	=ctg		α
R		2

	1
|SC|=R*ctg		α
	2

	1		1
PABC=R*R*ctg		α=R2*ctg		α
	2		2

	1
PAFS=		R2*sinα
	2

Pole wycinka FSDR

	180o−2α		π(90o−α
PFSDR=		*πR2=		*R2
	360o		180o

	1		π(90o−α
PFRDC=R2*ctg		α−R2*sinα−		*R2
	2		180o

	1		π(90o−α)
PFRDC=R2(ctg		α−sinα−		)
	2		180o

SAIzou:

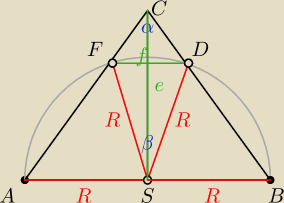
	α		e		α
ctg(		) =		→e = Rctg(		)
	2		R		2

	β
β = 180−2α →		= 90−α
	2

	1   f 2
sin(90−α)=
	R

	f
cosα =		→ f = 2Rcosα
	2R

Czworokąt CDSF jest deltoidem, zatem

	1		1		α		α
P(CDSF) =		ef =		*Rctg(		)*2Rcosα = R2cosα*ctg(		)
	2		2		2		2

	180−2α		90−α
P(wyc. DSF) = πR2*		= πR2*
	360		180

	α		90−α
P(t. na zewnątrz) = R2cosα*ctg(		) − πR2*		=
	2		180

	α		90−α
R2(cosα*ctg(		) − π		)
	2		180

Mi Ka: Witam i dzięki .