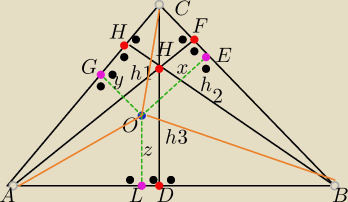
Trójkąt i punkt Mi Ka: Punkt O leży wewnątrz trójkąta ABC Odległości tego tego punktu od boków trójkąta sa odpowiednio równe x,y,z a wysokości sa równe h₁,h₂, h₃. Dowieść że:

x		y		z
	+		+		=1
h1		h2		h3

S_AOC+S_BOC+S_AOB=S_ABC

	1		1		1		1
1*)		AC*y+		BC*x+		AB*z=		BC*h1
	2		2		2		2

AC*y		x		AB*z
	+		+		=1
BC*h1		h1		BC*h1

	1		1		1		1
2*)		AC*y+		BC*x+		AB*z=		AC*h2
	2		2		2		2

y		BC*x		AB*z
	+		+		=1
h2		AC*h2		AC*h2

	1		1		1		1
3*)		AC*y+		BC*x+		AB*z=		AB*h3
	2		2		2		2

AC*y		BC*x		z
	+		+		=1
AB*h3		AB*h3		h3

Stąd z (1^*,2^*,3^*)

x		y		z
	+		+		=1
h1		h2		h3

wredulus_pospolitus: przeskoczona kwestia czemu 'znikają' pozostałe ułamki ... ale tak ... zgadza się.

Mi Ka: Witam . dzięki