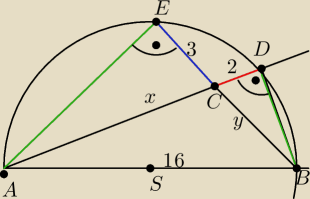
xxxxx Mi Ka: W trójkącie rozwartokątnym najdłuższy bok ma długość 16cm ,a spodki wysokości poprowadzonych z obydwu jego końców na pozostałe boki są odległe od wierzchołka kąta rozwartego o 2cm i o3cm. Oblicz długośi pozostałych boków . Wskazówka . Skorzystać z twierdzenia o przecinających sie cięciwach w okregu |AC|=x>0 |BC|=y >0 |CD|=2cm CE|=3cm |AB|=16 cm ∡|ADB|=90^o ∡|AEB|=90^o Obliczyc |AC| i |BC|. Z powyższego twierdzenia mamy |AC|*|CD|=|BC|*|CE| 2*x=3*y Z trójkata BDC |BD|²=y²−4 Z trójkata ADB |BD|²=16²−(x+2)² y²−4=256−x²−4x−4 y²+x²+4x−256=0 2x=3y

	3
x=		y
	2

	9
y2+		y2+6y−256=0
	4

	1
3		y2+6y−256=0
	4

13
	y2+6y−256=0
4

13y²+24y−1024=0 Δ=24²−((4*13*(−1024))=576+53248=53824 √Δ=232 y₁={−24−232}{26}<0 odpada

	−24+232
y2=		=8
	26

|BC|=y=8cm 2x=3y 2x=3*8=24 x=12 cm |AC|=x=12 cm

chichi: przecież masz odpowiedzi do zadań?

Mi Ka: No tak. Sa do zadań odpowiedzi i niekiedy także wskazówki Ale tez chodzi o to czy dobra jest metoda rowiązania