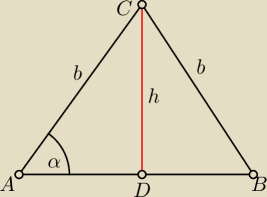
Trójkat równoramienny Mi Ka: W trójkącie równoramiennym suma ramienia i wysokości wynosi (s) a kąt przy podstawie wynosi (α) . Znależc pole powierzchni trójkata W odpowiedzi jest tak

	s2sin(2α)
P=		=1,44√3
	2(1+sinα)2

SAIzou:

	1		1
P=		*b2*sin(180−2α) =		*b2*sin(2α)
	2		2

	h
sinα =		⇒h = bsinα
	b

b+h = s b+bsinα=s

	s
b =
	1+sinα

	s2*sin(2α)
P =
	2(1+sinα)2

Mi Ka: Ach. Dzięki Nad wzorem nad pole pomyślalem ale potem liczyłem sinα i cosα i sie troche pogubiłem .