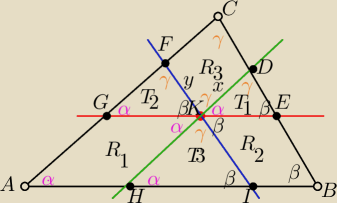
Pole trójkata Krzysiek Z: Przez punkt (K) leżący wewnątrz trójkąta poprowadzono trzy proste równoległe do boków trójkąta . Proste te dzielą ten trójką na trzy trójkąty T₁,T₂,T₃ oraz na trzy równoległoboki R₁,R₂ R₃. Wiedząc że pola powierzchni otrzymanych równoległoboków wynoszą odpowiednio P_r1.P_r2, P_r3 znależć pola powierzchni otrzymanych trójkątów W rónoległoboku R₃ |KD|=|FC|=x |CD|=KF|=y Pole rownolegloboku R₃ P_r3 =x*y *sinγ Do niego są przyległe trójkąty T₁ i T₂ Teraz jest napisane że 4P{T1}*P_T2=P_r3² Jak do tego dojść ? Dziękuje za odpowiedz

ite:

	1
PT1=		* x *|DE|*sin γ
	2

	1
PT2=		* y *|GF|*sin γ
	2

wtedy

	1		1
PT1*PT2=		* x *|DE|*sin γ *		* y *|GF|*sin γ
	2		2

zauważamy że ΔGFK∼ΔKDE (kkk)

	|GF|		x
stąd		=		→ x*y = |DE|*|GF|
	y		|DE|

podstawiamy

	1		1
PT1*PT2=		*		* x*y*x*y* sin γ * sin γ
	2		2

	1
PT1*PT2=		*PR3*PR3
	4

Krzysiek Z: Dzień dobry ite Dziękuje .

ite:

Mila: Masz odpowiedź w książce?

Mi Ka: Dzień dobry Milu Pozdrawiam. Jest tylko napisane tak 1)4P_T1*P_T2=P_R3}² 2) 4P_T2*P_T3=P_R1² 3)4P_T1*P_T3=P_R2² Z równań tych wyznaczamy

	PR2*PR3
PT1=
	2PR1

	PR1*PR3
PT2=
	2PR2

	PR1*PR2
PT3=
	2PR3

Są takie malutkie literki i cyfry ze miałem problem z odczytaniem ale sie udało

Mila: No i w porządku. Ite pokazała jak wyznaczyć pierwszy wzór , czy to jest jasne dla Ciebie? Pozostałe zależności w podobny sposób trzeba zrobić, Ja trochę inaczej to zrobiłam, jeśli chcesz to napiszę. Dalej problem z wyznaczeniem [T₁],[T₂], [T₃] z tym masz problem? ,

Mi Ka: Milu Tak. Jeśli możesz to proszę napisać swoje rozwiązanie . dziękuje .

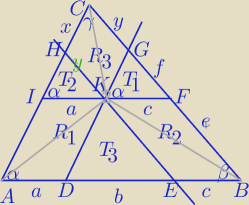Mila: ozn. [T₁]− pole ΔT₁ 1) Trójkąty: T ₁, T₂ , T ₃ są podobne do ΔABC 2) ΔADK i T₃

[T3]		b		2[T3]		b
	=		(Δ mają taką samą wysokość)⇔		=
12[R1]		a		[R1]		a

ΔT₃∼ΔT₂⇔

[T3]		b
	=(		)2
[T2]		a

===============

4[T32]		[T3]
	=		⇔
[R12]		[T2]

[R₁]²=4*[T₃]*[T₂] 3) ΔT₃ i R₂

[T3]		b		2[T3]		b
	=		⇔		=
12[R2]		c		[R2]		c

ΔT₃ i ΔT₁

[T3 ]		b
	=(		)2⇔
[T1]		c

4[T32]		[T3]
	=		⇔
[R22]		[T1]

[R₂]²=4*[T₃]*[T₁] 4] ΔT₁ i R₃

[T1]		f		2[T1]		f
	=		⇔		=
12[R3]		y		[R3]		y

ΔT₁ i ΔT₂

[T1 ]		f
	=(		)2
[ ΔT2]		y

====================⇔

4[T1]2		[T1 ]
	=		⇔
[R3]2		[ ΔT2]

R₃²=4*[T₁]*[T₂] ===================== 5)[

R32		4*[T1]*[T2]		[R3]2*[T3]
	=		⇔T2=
R22		4*[T3]*[T1]		[R2]2

[R₁]²=4*[T₃]*[T₂]

	R32*T3
[R1]2=4*[T3]*
	[R2]2

	[R1]*[R2]
[T3]=
	2[R3]]

======================== pozostałe w podobny sposób Bardzo źle mi się pisało w tym edytorze. Może nie będzie literówek.

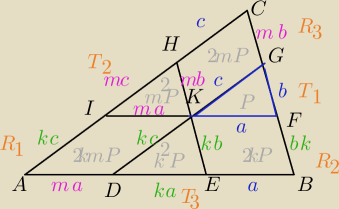SAIzou: ΔKFG ~ ΔDEK (kkk) w skali k, wówczas mamy DE = ka EK = kb DK = kc ΔKFG ~ ΔIKH (kkk) w skali m, wówczas mamy IK = ma KH = mb IH = mc Zatem mogę wszystkie pola uzależnić od k,m oraz pole trójkąta KFG = P (oznaczone na rysunku). [R1] = 2kmP

	[R2]
[R2] = 2kP → k =
	2P

	[R3]
[R3] = 2mP → m =
	2P

	[R2]		[R3]
[R1] = 2*		*		* P
	2P		2P

	[R2]*[R3]
[R1] =
	2P

	[R2]*[R3]
P =
	2[R1]

Mila: Też tak zaczęłam. Ustaliłam, że: P_ABC=(√[T₁]+√[T₂]+√[T₃])² Dalej nie liczyłam.

Mi Ka: Dziękuje za odpowiedzi Liczyłem inne zadanie z geometrii analitycznej i przy okazji oglądam serial i nie zagładalem na forum . Przepraszam