 Oblicz trzeci bok
Trzy cięciwy okręgu o promieniu r tworza trójkąt wpisany w ten okrąg .
Oblicz trzeci bok
Trzy cięciwy okręgu o promieniu r tworza trójkąt wpisany w ten okrąg .
| 1 | ||
Wiedzą że dwie z tych cięciw maja długość | r i r√3 znaleć długość trzeciej cięciwy | |
| 2 |
| 1 | ||
a= | r | |
| 2 |
| 1 | 1 | |||
c2= | r2+3r2−2* | r*√3r*cosγ | ||
| 4 | 2 |
| 1 | ||
c2=3 | r2−√3r2*cosγ | |
| 4 |

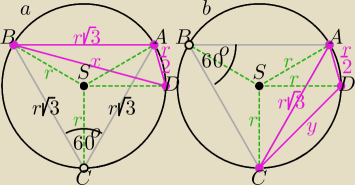 Są dwa przypadki: a) i b). Trójkąt ABC jest równoboczny, |∡ASB| = |∡ASC| = 120o.
Przyjemnej zabawy
Są dwa przypadki: a) i b). Trójkąt ABC jest równoboczny, |∡ASB| = |∡ASC| = 120o.
Przyjemnej zabawy 

| √3 | ||
x2=2r2+2 | r2 | |
| 2 |
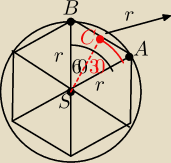 Witam.
Troche mi nie wyszedł rysunek
|AB|=r i kąt srodkowyASB =60o
Witam.
Troche mi nie wyszedł rysunek
|AB|=r i kąt srodkowyASB =60o
| 1 | ||
|AC|= | r to kąt srodkowy ASC=30o | |
| 2 |
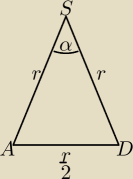 z twierdzenia cosinusów: cosα = ?
z twierdzenia cosinusów: cosα = ?
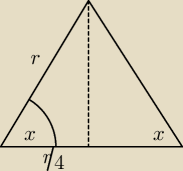 Liczyłem też to troche inaczej
Liczyłem też to troche inaczej
| r/4 | 1 | |||
cosx= | = | |||
| r | 4 |

| r | r | 1 | 1 | |||||
(r√3)2=( | )2+y2−2* | *y*(− | ) bo cos120o=−sin30o=− | |||||
| 2 | 2 | 2 | 2 |
| 1 | 1 | |||
3r2= | r2+y2+ | ry | ||
| 4 | 2 |
| 1 | 3 | |||
−y2− | ry+2 | r2=0 | ||
| 2 | 4 |
| ry | 11 | |||
y2+ | − | r2=0 | ||
| 2 | 4 |
| −2−6√5r | ||
y1= | <0 odpada | |
| 8 |
| −2+6√5r | 2(3√5r−1) | 3√5−1 | ||||
y2= | = | = | >0 dobry | |||
| 8 | 8 | 4 |
| r | ||
|AS|=r |BD|=x |AB|=r√3 |SD|=r |SB|=r |AD|= | ||
| 2 |
| 1 | ||
r*x=r2√3+ | r2 | |
| 2 |
| 1 | ||
r*x=r2(√3+ | ) | |
| 2 |
| 1 | ||
x=r(√3+ | ) | |
| 2 |

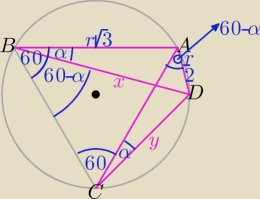 No dobra, jedziemy.
No dobra, jedziemy.
| 1 | √15 | ||||||||||
W trójkącie ABD z twierdzenia sinusów: | =2r ⇒ sinα= | , cosα= | ||||||||||
| sinα | 4 | 4 |
| √3 | √15 | 1 | 1 | 3√5 + 1 | ||||||
sin(60o + α) = | * | + | * | = | ||||||
| 2 | 4 | 4 | 2 | 8 |
| √3 | √15 | 1 | 1 | 3√5 − 1 | ||||||
sin(60o − α) = | * | − | * | = | ||||||
| 2 | 4 | 4 | 2 | 8 |
| x | ||
w trójkącie BCD: | = 2r ⇒ x = ... | |
| sin(60o + α) |
| y | ||
w trójkącie ACD: | = 2r ⇒ y = ... | |
| sin(60o − α) |
