Trójkąt równoramienny
Krzysiek Z:
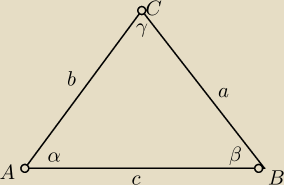
Wykazac że jeżeli w trójkącie zachodzi związek
| sinα | |
| =2cosγ to trójkąt jest równoramienny |
| sinβ | |
α=18o
o−(β+γ)
sinα=sin[180
o−(β+γ)]=sin(β+γ)
sin(β+γ)=2cosγ*sinβ]
sinβ*cosγ+cosβ*sinγ=2sinβ*cosγ
cosβ*sinγ=cosγ*sinβ
cosβ*sinγ−cosγ*sinβ=0
−[sin(β−γ)]=0 dla β=y
Dwa kąty sa równe więc trójkat jst równoramienny