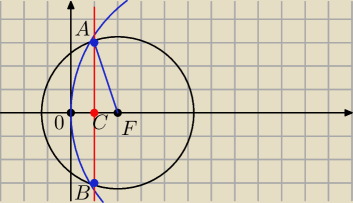
Parabola i okrąg Krzysiek Z: Parabola y²=4ax a>0 i okrąg o środku (a,0) mają wspólna cięciwę jednakowo odległą od wierzchołka paraboli i od środka okręgu. Napisz równanie tego okręgu |OF|=a

	1
Ogniskową paraboli y2=2px jest punkt F(		p,0)
	2

	1
2p=4a p=2a		p=a
	2

	1
Daje nam to ze punkt F (		p,0) jest też srodkiem szukanego okręgu
	2

Równanie okręgu ma postac (x−a)²+(y−0)²=r² (promien jest nieznany

	1
Z warunków zadania mamy także to że równanie cięciwy jest postaci x=		a
	2

Dostajemy układ równań {y²=4ax

	1
{x=		a
	2

	1
y2=4*a*		a=2a2
	2

y=√2a oraz y=−√2a

	1
Punkt A ma współrzedne A(		a,√2a)
	2

	1
Punkt B ma wspólrzedne B(		a,−√2a)
	2

W trójkącie ACF FA²=r²

	1
|CF|=		a
	2

|CA|=√2a

	1		1		9
FA2=(		a)2+(√2a)2=		a2+2a2=		a2 =r2
	2		4		4

Okrąg ma równanie

	9
(x−a)2+y2=		a2
	4