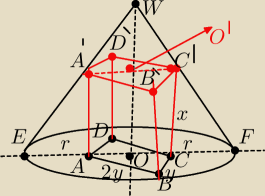
Stożek i prostopadłościan Tygrys i żuraw: Długość promienia podstawy stożka wynosi r ,a wysokość zaś h . W stożku tym umieszczono prostopadłościan w ten sposób że jego podstawa zawarta jest w podstawie stożka a wierzchołki drugiej podstawy należą do powierzchni bocznej stożka . Stosunek długości krawędzi podstawy wynosi 2. Obliczyć długość krawędzi prostopadłościanu o największej objętości AB=DC=A'B'=D'C'=2y BC=B'C'=AD=A'D'=y CC'=x −wysokośc prostopadłościanu EO=OF=r −promień podstawy stożka OW=h wysokośc stożka Objętośc prostopadłościanu V=2y*y*x=2y²*x Wyrażmy ją za pomoca (x) Rozpatrzmy dwa trójkąty podobne Δ A'C'W i Δ EFW Mamy tu A'C'=√y²+4y=y√5 WO'=h−x EF=2r WO=h

A'C'		EF
	=
WO'		WO

y√5		2r
	=
h−x		h

y√5*h=2r(h−x) 5y²*h²=4r²*(h−x)²

	4r2(h−x)2
y2=
	5h2

	4r2(h−x)2		8r2(h−x)2*x		8r2
V=2*		*x=		=		*x(h−x)2
	5h2		5h2		5h2

Objętość tego prostopadłościanu będzie największa dla takiej wartości x dla której f(x)=x(h−x)² ma wartośc największa Reszte postaram sie dokonczyć juz pózniej . Ktos sprawdzi czy do tej pory jest dobrze . dziękuje

Tygrys i żuraw: f(x)=x(h−x)²=x(h²−2hx+x²)=x³−2hx²+h²x (x³−2hx²+h²x)'=3x²−4hx+h² dla x>0 h>0 i h>x czyli 0<x<h 3x²−4hx+h²=0 Δ=16h²−12h²=4h² √Δ=2h

	4h−2h		1
x1=		=		h spełnia warunki zadania
	6		3

	4h+2h
x2=		=h nie spełnia warunku dziedziny
	6

	4r2
y2=		*(h−x)2
	5h2

	2r
y=		*(h−x)
	√5h

	2r		2h		4r		4√5r
y=		*		=		=
	√5h		3		3√5		15

	8√5r
2y=
	15

x=U[1}{3}h Prosze o sprawdzenie i ewentualnie o komentarz gdzie żle i dlaczego . dziękuje

Mila: Ładny rysunek Sprawdzę, gdy się ochłodzi.

Krzysiek Z: Dzień dobry U mnie jest 30^o i tez na razie sobie odpuszczam