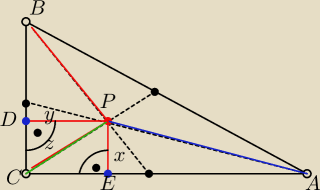
Trójkąt prostokatny Tygrys i żuraw: W trójkącie prostokątnym ABC o kącie prostym przy wierzchołku C obrano punkt P tak, aby trójkąty PAB, PBC, PAC miały równe pola Obliczyc PC mając dane m=PA²+PB² S_PAC=S_PCB=S_PAB(1^*) PA²+PB²=m (2^*) ∡BCA=90^o Oznaczam PE=x i PE⊥AC (będzie to wysokość ΔPCA PD=y i PD⊥BC (będzie to wysokość ΔPCB Na teraz mam dwa pytania Nr1) Jeśli te trzy pola maja być jednakowe to tym punktem P będzie punkt przecięcia się środkowych? Nr2) W szkicu rozwiązania jest napisane

1		1
	AC*x=		AC*BC−−−−−−−−−−−−−−−−−−−BC=3x
2		6

	1
Czemu to jest		AC*BC?
	6

	1		1
Czy może dlatego ze SABC=		AC*BC a SPAC=		SABC?
	2		3

Tygrys i żuraw: Pewnie będzie tak To dalej tym tokiem rozumowania

1		1
	BC*y=		AC*BC−−−−−−−−−−−−−−−AC=3y
2		6

AE=AC−PD=3y−y=2y DB=BC−PE=3x−x=2x W trójkącie PEA PA=√x²+4y² to PA²=x²+4y² W trójkącie PDB PB=√y²+4x² to PB²=y²+4x² PA²+PB²=m x²+4x²+y²+4y²=m 5x²+5y²=m 5(x²+y²)=m

	m		1
x2+y2=		=		m
	5		5

Ale x²+y²=z² =PC² stad PC=√¹₅m}