Okrąg wpisany w trójkąt
Dong:
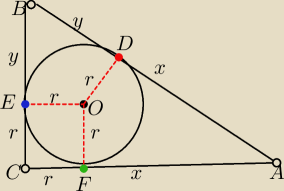
Wykazać ze okrąg wpisany w trójkąt prostokątny jest styczny do przeciwprostokątnej w punkcie
dzielącym
przeciwprostokątną na dwa odcinki .których iloczyn długości jest równy polu powierzchni tego
trójkąta
|AD|=|AF|=x
|BD|=|BE}=y
|CE=CF|=r z twierdzenia o stycznych do okręgu
Obwód=2p=2x+2y+2r=2(x+y+r)
p=x+y+r
P=p*r=(x+y+r)*r (1
*)
===========
Z twierdzenia Pitagorasa
|CA|
2+|BC|
2=|AB|
2
(x+r)
2+(y+r)
2=(x+y)
2
(x+y)
2=(x+r)
2+(y+r)
2
x
2+2xy+y
2=x
2+2xr+r
2+y
2+2yr+r
2
2xy=2xr+2yr+2r
2
xy=xr+yr+r
2
xy=r(x+y+r) (2
*)
Z porównania (1
*)i (2
*) P=x*y=|AD|*|BD|
 Wykazać ze okrąg wpisany w trójkąt prostokątny jest styczny do przeciwprostokątnej w punkcie
dzielącym
przeciwprostokątną na dwa odcinki .których iloczyn długości jest równy polu powierzchni tego
trójkąta
|AD|=|AF|=x
|BD|=|BE}=y
|CE=CF|=r z twierdzenia o stycznych do okręgu
Obwód=2p=2x+2y+2r=2(x+y+r)
p=x+y+r
P=p*r=(x+y+r)*r (1*)
===========
Z twierdzenia Pitagorasa
|CA|2+|BC|2=|AB|2
(x+r)2+(y+r)2=(x+y)2
(x+y)2=(x+r)2+(y+r)2
x2+2xy+y2=x2+2xr+r2+y2+2yr+r2
2xy=2xr+2yr+2r2
xy=xr+yr+r2
xy=r(x+y+r) (2*)
Z porównania (1*)i (2*) P=x*y=|AD|*|BD|
Wykazać ze okrąg wpisany w trójkąt prostokątny jest styczny do przeciwprostokątnej w punkcie
dzielącym
przeciwprostokątną na dwa odcinki .których iloczyn długości jest równy polu powierzchni tego
trójkąta
|AD|=|AF|=x
|BD|=|BE}=y
|CE=CF|=r z twierdzenia o stycznych do okręgu
Obwód=2p=2x+2y+2r=2(x+y+r)
p=x+y+r
P=p*r=(x+y+r)*r (1*)
===========
Z twierdzenia Pitagorasa
|CA|2+|BC|2=|AB|2
(x+r)2+(y+r)2=(x+y)2
(x+y)2=(x+r)2+(y+r)2
x2+2xy+y2=x2+2xr+r2+y2+2yr+r2
2xy=2xr+2yr+2r2
xy=xr+yr+r2
xy=r(x+y+r) (2*)
Z porównania (1*)i (2*) P=x*y=|AD|*|BD|
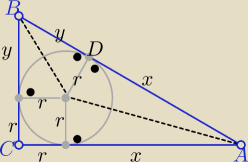 2P= (x+r)(y+r) i P= r2+xr+yr
2P= xy+xr+yr+r2
2P=xy+P
P=xy
======
2P= (x+r)(y+r) i P= r2+xr+yr
2P= xy+xr+yr+r2
2P=xy+P
P=xy
======

