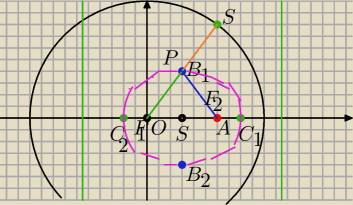
Równanie krzywej Dong: Wyznaczyć równanie krzywej będącej zbiorem wszystkich punktów ,których odległości od okręgu x²+y²=100 i od punktu A(6,0) są równe . Naszkicuj tę krzywą OS=10 A=(6,0) P(x,y) S(x,√100−x²) |PS|=|PA| |PS|=|OS|−|OP| |OP|=√(x−0)²+(y−0)²=√x²+y² |PS|=10−√x²+y² |PA|=√(x−6)²+(y−0)²+√(x−6)²+y² 10−√x²+y²=√(x−6)²+y² (10−√x²+y²)²=(√(x−6)²+y²)² 100−20√x²+y²+x²+y²=x²−12x+36+y² 100−20√x²+y²=36−12x −20√x²+y²=−64−12x 400(x²+y²)=144x²+1536x+4096 256x²+400y²=1536x+4096 16x²+25y²=96x+256 16x²−96x+25y²=256 16(x²−6x)+25y²=256 16(x−3)²+25y²−16*9=256 16(x−3)²+25y²=400

(x−3)2		y2
	+		=1
25		16

Jest to równanie elipsy Srodek elipsy w punkcie S(3,0) Półos a=5 Półos b=4 Ogniskowa c=3

	3
Momośród e=
	5

	1
Kierownice x=−5		i x=11U{1}[3
	3

Ogniska F₁(0,0) F₂(6,0)=A (6,0) Wierzchołki elipsy B₁(3,4) B₂(3,−4) C₁(8,0) C₂(−2,0) Elipsa troche koślawa