Elementarne równania trygonometryczne Krzysiek: Taki problem . Jest np równanie postaci

	√3
sin(x)=
	2

	π
sin(x)=sin
	3

	π		π		2
x=		+2kπ lub x=(π−		)+2kπ=		π+2kπ k∊C
	3		3		3

Tutaj nie mam z tym problemu Teraz mam równanie np takie

	√3
sin(x)=−
	2

Pytanie moje jest takie . Czy moge zapisać to tak (zapomiałem wykresu funkcji sinius )

	π
sin(x)=sin(−		)
	3

	π		π		π		4
x=−		+2kπ lub x=[π−(−		)]=π+		=		π+2kπ
	3		3		3		3

Czy należałoby to inczej przekształcać?

wredulus_pospolitus: tak jak jest ... jest ok.

wredulus_pospolitus: chociaż lepiej już oba zapisy mieć w tej samej ćwiartce czyli albo −π/3 i −2π/3 bądź (odpowiednio) 5π/3 i 4π/3

Krzysiek: Bardzo dziękuje CI za odpowiedz.

chichi: i ten ciąg równości w drugim członie alternatywy nie zachodzi...

Krzysiek:

	3π		π		9π		2π		11π
x=		+		=		+		=
	2		3		6		6		6

	4		11
Bądz odpowiednio (		π+2kπ i		π+2kπ).
	3		6

Trochę się pomylił . Ale juz dzięki Tobie mamy to skorygowane Równania tgx=k i ctgx=k maja po jednym rozwiązaniu x=α+k*π Tutaj nie mam z tym problemu . ======= Kąty spełniające równanie cos(x)=p ( −1<p<1) wyrażone sa wzorami x₁=α+k*2π oraz x₂=−α + k*2π ============================= Wezme równanie

	1
cos(x)=
	2

	π
cosx=cos(
	3

	π		π
x1=		+k*2π lub x2=−		+k*2π
	3		3

Pytanie . Proszę o pokazanie jak tym schematem rozwiązania rozwiązac równanie

	1
cos(x)=−
	2

	π
cos(x)=−cos(
	3

	π		π		π
x1=−		+k*2π lub x2=−(−		)+k*2π=		+k*2π (a to nie jest równe juz
	3		3		3

	1
(−		)
	2

.: Ogólnie to warto znać wzory redukcyjne sin(−x) = − sinx cos(−x) = − cos(x + π)

.: Więc jeżeli cosx = − 0.5 To mamy cos(x+π) = 0.5

chichi: no bo jakim prawej porównujesz argumenty skoro masz różne funkcje... cos(x) to nie to samo co −cos(x)...

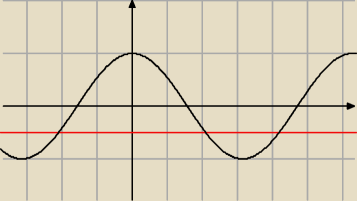
Krzysiek: Dobry wieczór Z wykresu mogę odczytać bez problemu Jednak jak to zrobić bez wykresu ? cos(−x)=cosx cos(x+π)=−cosx cos(π−x)=−cosx Więc jeśli by do tego równania

	1
cos(x) =−		zastosować wzory redukcyjne tak jak proponuje kolega to można byłoby zapisać
	2

tak

	1
cos(x)=−
	2

	π		π
cos(x)=cos(π−		) lub cos(x)=cos(π+		)
	3		3

	2		4
x=		π+k*2π lub x=		π+k*2π
	3		3

Teraz byłoby w porządku?

chichi: przeczytaj mój wpis... jeśli chcesz tak poczynić to musisz całą te wartość razem z minusem

	1		2π
przedstawić jako cosinusa pewnego argumentu, np. −		= cos(		) i dopiero
	2		3

porównywać...

Krzysiek: chichi Czyli tak jak napisałem o 19 : 01? I tak samo jesli mamy p∊(−1,0) dla sinusa tez wzory redukcyjne .

chichi: piszesz o innej metodzie, a rozpisujesz inną. chcesz korzystać z parzystości cosinusa rozwiązując równanie, a wcale z tego nie korzystasz. wzór redukcyjny służył Ci do złapania x₀, czyli do rozwiązania szczególnego, a wtedy nie próbujesz złapać kolejnego, tylko korzystasz z parzystości.

	1		π		2π
cos(x) = −		⇔ cos(x) = cos(π −		) ⇔ cos(x) = cos(		), a więc:
	2		3		3

	2π		2π
x =		+ 2kπ ∨ x = −		+ 2kπ, gdzie k ∊ ℤ.
	3		3

Krzysiek: Dobrze . Teraz rozumiem . Dziękuje bardzo za wyjaśnienie

chichi: dobrej nocy