BARDZO PROSZĘ O POMOC MACIEK: Oblicz wysokość trójkąta opisanego na boku długości 12, jeżeli kąty przy tym boku są równe 30 stopni i 45 stopni

wredulus_pospolitus:

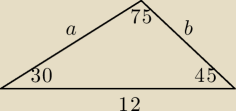
	b		a		12
Z tw. sinusów:		=		=
	sin30		sin45		sin75

natomiast sin75 = sin(30+45) = sin30cos45 + cos30sin45 = ...

Little Mint: Popraw treść zadania . Trójkąt nie może byc opisany na boku . Może być opisany na okręgu

MACIEK: Takie dostałem polecenie i tak jest w nim napisane, więc nie mogę nic tu zmienic.

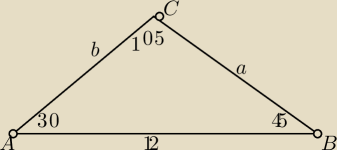
Little Mint: Może ma byc Oblicz wysokośc trójkąta opusczoną na bok 12 itd .. Popraw także rysunek W trójkącie suma kątów wewnetrzych wynosi 180^o W trójkącie naprzeciwko mniejszego kąta leży mniejszy bok Wredulus pewnie miał na myśli wzory redukcyjne i z rozpędu zaznaczył 75^o bo sin(105^o)=sin(90^o+15^o)=cos15^o lub sin(105^o)=sin(180^o−75^o)=sin75^o

Little Mint: AB=c=12 Z twierdzenia sinusów

a		12
	=
sin30o		sin75o

	sin30o*12
a=
	sin75o

sin(75^o)=sin(30^o+45^o)= sin30^o*cos45^o+cos30^o*sin45^o

	1		√3		√2
sin30o=		cos30o=		sin45o=cos45o=
	2		2		2

	1		√2		√3		√2
sin75o=		*		+		*		=
	2		2		2		2

√2		√6		√2+√6
	+		=
4		4		4

===============

	(1/2)*12		6*4		24		24(√6−√2
a=		}=		=		=		=
	√2+√6   4		√2+√6		√6+√2)		6−2

	24(√6−√2)
=		=6(√6−√2)
	4

========================

	1
Pole trójkata ABC=		*a*c*sin45o
	2

	1		√2
PABC=		*6(√6−√2)*12*		=
	2		2

	36(√6−√2)
=		=18(√6−√2) [j2]
	2

==================

	1		c*h
Z drugiej strony PABC=		*c*h=		gdzie h to wysokośc tego trójkata
	2		2

2P_ABC=c*h

	2PABC
h=
	c

h=2*18(√6−√2}{12}

	36(√6−√2)
h=		= 3(√6−√2) [j]
	12

============== Sprawdz jeszcze raz rachunki bo liczyłem w pamięci

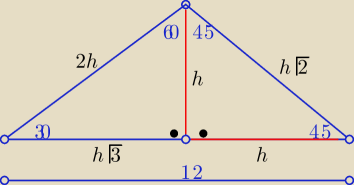
aa: Z własności trójkątów "ekierkowych" (oznaczenia na rys.) h√3+h=12 h(√3+1)=12 h=6(√3−1) ========= i po ptokach

aa: @Littt masz błąd w obliczeniu pola P_ABC= 36(√3−1) ====================

Little Mint: OK

MACIEK : Czyli wersja aa: jest dobra?

Jolanta: Oczywiście

Jolanta: Jak masz trójkąt prostokątny o kątach 30 ⁰ i 60 ⁰ to na przeciwko kat 30 ⁰ jest bok o długości a Na przecieki 60⁰ bok o długości a√3 a na przeciwko 90⁰ bok o długości 2a

Little Mint:

	√2
Tak. Licząc pole nie domnożyłem przez
	2