Geom Mat: Punkty A(−1,1) B(1,0) C(−1,2) Są wierzchołkami trójkąta Abc Wyznacz punkt P tak że {|AP|}{|AB|}={5}{6}

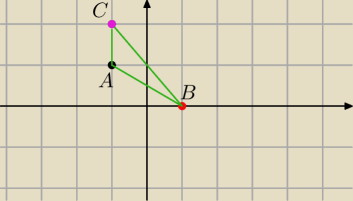
Li Muqin: Czy dobrze myśle do tego zadania ? Według mnie chodzi o znalezienie takiego punktu P na odcinku AB który go dzieli w stosunku

	5
	6

	5
Więc k=		.
	6

Jeśli tak to po co jest podany punkt C? Nie rozumiem tego .

wmboczek: stosunek niezbyt poprawnie podany rzeczywiście C zbędne Rozwiązaniem jest okrąg o środku A, może powinno być coś o P np. leży na prostej BC

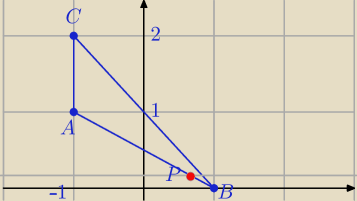
Mila: Jeśli P∊AB 1) AB^→=[2,−1]

	5		10		5
AP→=		[2,−1]=[		,−		]
	6		6		6

	5		5		2		1
A=(−1,1)→T{{5/3,−5/6]}⇔P=(−1+		,1−		]=(		,		)
	3		6		3		6

Oblicz dł.AP , AB i sprawdź podany warunek 2) Podział odcinka w danym stosunku ( def. ) : k>0

AP
	=k
PB

AP→=k*PB^→

Li Muqin: Dziękuje Milu Pozdrawiam .

Mila: Proszę, "chińczyk" działa. Pozdrawiam Pisz jeśli w odpowiedzi jest inaczej.