Geometria konkursowa Michał: W trójkącie równobocznym ABC o boku długości a punkt D należy do boku BC i BD = 2CD . Symetralna odcinka AD przecina bok AB w punkcie P oraz bok AC w punkcie R. Oblicz długość odcinka PR. Z góry dzięki za pomoc

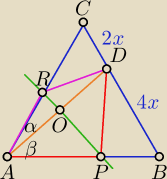
chichi: dla łatwości obliczeń, niech a = 6x. (1) z tw. cosinusów w ΔABD bądź ΔCAD mamy, że |AD| = 2√7x (2) z tw. sinusów w ΔABD mamy:

4x		2√7x		√3		2
	=		⇒ sinβ =		⇒ cosβ =
sinβ		sin60o		√7		√7

	√7x		7
(3) w ΔAOP mamy: cosβ =		i podstawiając wynik z (2) wychodzi, że |AP| =		x
	|AP|		2

(4) z tw. sinusów w ΔADC mamy:

2x		2√7x		√3		5
	=		⇒ sinα =		⇒ cosα =
sinα		sin60o		2√7		2√7

	√7x		14
(5) w ΔAOR mamy: cosα =		i podstawiając wynik z (4) wychodzi, że |AR| =		x
	|AR|		5

(6) czworokąt APDR jest deltoidem, a zatem porównajmy jego pole na dwa sposoby tj. :

	1		7		14		√3		1
|AP||AR|sin60o =		|PR||AD| ⇔		x *		x *		=		|PR| * 2√7x
	2		2		5		2		2

	49√3		49√3		a
a więc mamy, że |PR| =		x =		*		= ...
	10√7		10√7		6

Mila: Rozwiązałam trochę inaczej.

	1
Skorzystam z tego , że pole ΔCD jest równe		pola ΔABC.
	3

Obliczyłam sinα, potem cos(α). W podobny sposób obliczyłam sinβ, cosβ. Z tangensów: |RP|. Twoim sposobie chyba mniej obliczeń. Michał może spróbować .

chichi: michał chyba średnio zainteresowany, miejmy nadzieję, że komuś się to kiedyś przyda, a nie wklepane na marne..

wmboczek: Ja myślałem o osadzeniu ABC w układzie wsp. i wykorzystaniu geometrii analitycznej ale zapisać tego na forum się nie chce