dowód geometryczny
PelsynWan: Dany jest czworokąt wypukły 𝐴𝐵𝐶𝐷. Przekątne 𝐴𝐶 oraz 𝐵𝐷 tego czworokąta przecinają
się w punkcie 𝑆.
| | |𝐴𝑆| | | |𝐵𝑆| | |
Wykaż, że jeżeli |
| = |
| |
| | |𝐷𝑆| | | |𝐶𝑆| | |
, to na czworokącie 𝐴𝐵𝐶𝐷 można opisać okrąg.
26 maj 12:38
Aruseq: Z równości tej i kątów wierzchołkowych wynika podobieństwo trójkątów i to w zasadzie rozwiązuje
zadanie
26 maj 12:41
PelsynWan:
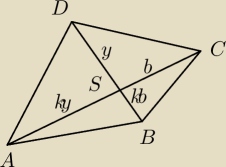
Teza:
|∡ABC|+|∡ADC|=180
oraz
|∡BAD+|∡BCD|=180
wtedy na czworokącie można opisać okrąg
ponieważ trójkąty ABS oraz DSC są podobne i mają podobne długości odpowiadających sobie boków
AS oraz DS i BS oraz CS to
|∡ASD|=α=|∡BSC|
|∡ABS|=β=|∡DCS|
|∡BAS|=γ=|∡CDS|
|∡DAS|=1'=|∡BCS|
|∡ADS|=2'=|∡CBS|
z przekształceń i obliczeń otrzymałem
β+γ=180−(1'+2')
α=β+γ
1'+2'=180−α
|∡ABC|+|∡ADC|=180−1'+2'
|∡BAD|+|∡BCD|=180−2'+1'
Potrzebuję wykazać, że 1'=2', lecz nie wiem jak do tego dojść.
Proszę o pomoc.
Pozdrawiam
14 cze 11:47
aa:
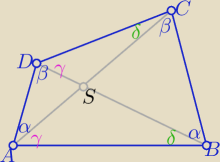
| | |AS| | | |BS| | | |AS| | | |DS| | |
Z treści zadania |
| = |
| oraz |
| = |
| |
| | |DS| | | |CS| | | |BS| | | |CS| | |
wiemy,że trójkąty : ASD i BSC oraz ASB i DSC są podobne
z cechy (bkb) to i miary odpowiednich kątów są równe
oraz α+β+γ+δ=180
o
co kończy dowód ( bo sumy kątów przeciwległych są równe 180
o)
Na czworokącie ABCD można opisać okrąg
14 cze 21:00
Mila:

15 cze 00:19
Pelis: ok, dziękuję za pomoc! Pozdrawiam
23 cze 00:34
 Teza:
|∡ABC|+|∡ADC|=180
oraz
|∡BAD+|∡BCD|=180
wtedy na czworokącie można opisać okrąg
ponieważ trójkąty ABS oraz DSC są podobne i mają podobne długości odpowiadających sobie boków
AS oraz DS i BS oraz CS to
|∡ASD|=α=|∡BSC|
|∡ABS|=β=|∡DCS|
|∡BAS|=γ=|∡CDS|
|∡DAS|=1'=|∡BCS|
|∡ADS|=2'=|∡CBS|
z przekształceń i obliczeń otrzymałem
β+γ=180−(1'+2')
α=β+γ
1'+2'=180−α
|∡ABC|+|∡ADC|=180−1'+2'
|∡BAD|+|∡BCD|=180−2'+1'
Potrzebuję wykazać, że 1'=2', lecz nie wiem jak do tego dojść.
Proszę o pomoc.
Pozdrawiam
Teza:
|∡ABC|+|∡ADC|=180
oraz
|∡BAD+|∡BCD|=180
wtedy na czworokącie można opisać okrąg
ponieważ trójkąty ABS oraz DSC są podobne i mają podobne długości odpowiadających sobie boków
AS oraz DS i BS oraz CS to
|∡ASD|=α=|∡BSC|
|∡ABS|=β=|∡DCS|
|∡BAS|=γ=|∡CDS|
|∡DAS|=1'=|∡BCS|
|∡ADS|=2'=|∡CBS|
z przekształceń i obliczeń otrzymałem
β+γ=180−(1'+2')
α=β+γ
1'+2'=180−α
|∡ABC|+|∡ADC|=180−1'+2'
|∡BAD|+|∡BCD|=180−2'+1'
Potrzebuję wykazać, że 1'=2', lecz nie wiem jak do tego dojść.
Proszę o pomoc.
Pozdrawiam

