Ilość rozwiązań równania kwadratowego w zależności od parametru "m" Kokosz: Określ korzystając z metody graficznej ilość rozwiązań równania w zależności od parametru "m" Wykonaj wykres zależności ilości rozwiązań równania w zależności od "m" x² − mIxI = m² − 1 Jak tu wystartować?

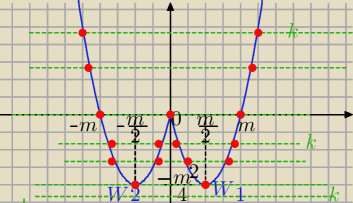
Kajko: W1=(m/2, −m²/4) W₂ =(−m/2, −m²/4) y=x²−m|x| miejsca zerowe x∊{−m,0,m} y= k= m²−1 0 rozwiązań dla m²−1< −m²/4 ⇒........... m∊(−2/√5, 2/√5)\ {0} 1 rozwiązanie dla m= 0 ( x²=0 ⇒ x=0) 2 rozwiązania dla m²−1> 0 lub m²−1 = −m²/4 ⇒ ..... m∊(−∞,−1)U(1,∞)U{−2/√5, 2/√5} 3 rozwiązania dla m²−1=0 ⇒ m= −1 v m=1 4 rozwiązania dla m²−1<0 ∧ m²−1> −m²/4 ⇒... m∊(−1,−2/√5)U (2/√5, 1)

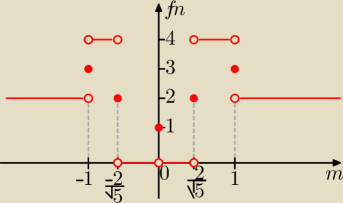
Kajko: wykres ilości rozwiązań w zależności od parametru "m"

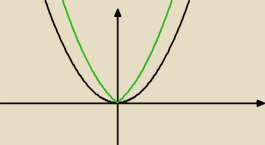
Kokosz: A czy nie uważasz, że powinno się rozpatrzyć od początku 3 warianty dla "m" tzn. m<0, m=0 i m>0? Twój wykres wg mnie jest poprawny dla m>0 Dla m=0 będzie y=x² (na czarno) Dla m<0 będzie y=x²−(−m)|x|=x²+m|x| (na zielono) Na tych wykresach faktycznie dla m=0 i m<0 dla y=0 jest jedno rozwiązanie, dla y>0 − są 2 rozwiązania. Ale jak to zauważyć na twoim wykresie − skąd (poza logicznym podejściem lub podstawianiem) doszedłeś do "1 rozwiązanie"?

Kokosz: A w ogóle i w szczególe − dzięki za podpowiedź w poprzednim poście odnośnie przeniesienia się w czasie Najpierw nie zrozumiałem aluzji − ale tak to już jest z byłymi szachistami Początki są trudne

Kokosz: Cześć Kajko Chwilę mnie tu nie było, ale teraz analizuję Twoje rozwiązanie i na wykresie funkcji nie widzę opcji z 1 rozwiązaniem Niech f(x) = x² − m|x| a g(x) = m² − 1 Dla m=0 wg mnie jest 0 rozwiązań (f(x) = x² a g(x) = −1 − na obecnym poziomie mojej nauki − nie ma rozwiązania bo zakładając f(x) = g(x) czyli x² = −1 nie znajduję odpowiedniej mocy, żeby to rozkminić) Może mi to jednak ktoś rozłoży jak krowie na rowie tak krok po kroku, bo już po prostu padłem. Nie jestem już pewien moich wypocin z 8 maja

wredulus_pospolitus: Wykres ok ... ale wnioski z wykresu nietrafione