Obraz Jaskiniowiec : Obrazem punktu P (1,3) w jednokładności o środku S −2,12 i skali s 5/3 jest punkt: jak to zrobić?

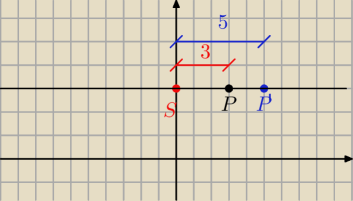
wredulus_pospolitus: Ogólnie (zastosuj to poprzez analogię do Twego zadania. 1. Zaznaczamy punkt P 2. Zaznaczamy punkt S 3. Prowadzimy prostą przechodzącą przez te dwa punkty 4. Wyznaczamy odległość |PS| = 3 (w przykładzie)

	5
5. wyznaczamy odległość |P'S| korzystając z odległości (4) i danej skali k =		...
	3

otrzymując odległość 5. 6. Zaznaczamy punkt P' na prostej tak aby spełniona była odległość UWAGA. Gdy skala k > 0 ; punkt pozostaje P' po tej samej stronie co punkt P (względem punktu S) Gdy skala k < 0 ; punkt jest P' po przeciwnej stronie co punkt P (względem punktu S) Teoria: https://zpe.gov.pl/a/przeczytaj/DXMJRR3lt

wredulus_pospolitus: Powyższe rozumowanie można zastosować tylko do patrzenia na różnice we współrzędnych punktów. W Twoim przypadku będziemy mieli P'(3, −3) ponieważ patrząc na współrzędne punktu P i S mamy różnicę: 3 i −9, więc po przeskalowaniu, różnica współrzędnych pomiędzy P' i S będzie 5 i −15. Jako, że skala k > 0 to punkt P' będzie po tej samej stronie co punkt P, więc jego współrzędne to P'(−2 + 5 , 12 − 15)

Jaskiniowiec : Odległość ps wyszła pierwiastek z 97 i jak mam to p prim s wyznaczyć i skorzystać z tej skali? Jak to wyszło w tym przykładzie 5?

Jaskiniowiec : W dałoby się to z wektorów zrobić czy niezbyt?

wredulus_pospolitus: oczywiście, że się da z wektorów ... z wektorów zrobisz dokładnie tak samo jak pokazałem o 20:00 ... ja po prostu nie zapisałem tego w postaci wektorowej

wredulus_pospolitus: a co do liczenia odległości |PS| = √9 + 81 = √90 = 3√10 to tak na marginesie

Eta:

	5
P=(1,2) , S=(−2,12) k=
	3

→ → SP^'=k*SP =========

	5
[x'+2, y'−12]=		[1+2,3−12]
	3

[x^'+2, y^'−12]= [ 5,−15] x^'=5−2 ∧ y^'= −15+12 x^'=3 ∧ y^'= −3 P^'=(3,−3) =========