liczenie objętości ostrosłupa z trapezem w podstawie abcd: Podstawą ostrosłupa jest trapez prostokątny o podstawach 6 i 30. Wysokości wszystkich ścian bocznych ostrosłupa są równe 5√5. Oblicz objętość tego ostrosłupa.

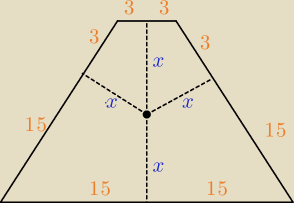
wredulus_pospolitus: 1. Rysunek 2. Skoro wszystkie wysokości ścian bocznych są sobie równe, to znaczy że spodek wierzchołka jest w 'połowie' trapezu, tak że jego odległość do każdej krawędzi podstawy jest taka sama (trochę rysunek mi nie wyszedł ) 3. Stąd znamy ramiona trapezu (przystawanie trójkątów). 4. Możemy opuścić wysokość z wierzchołka krótszej podstawy, mamy trójkąt prostokątny, znamy jego dwa boki ... wyznaczamy wysokość (2x) trapezu 5. Znamy wysokość ściany bocznej, znamy 'x' ... możemy z Pitagorasa wyznaczyć h_ostrosłupa 6. Bierzemy wzór na objętość i gotowe.

wredulus_pospolitus: ajjj ... zrobiłem wersję z trapezem równoramiennym zmienić rysunek trzeba

abcd: znaczy tam miał być chyba prostokątny i wtedy to chyba nie idzie tak gładko

abcd: bo mi się wydaje że wtedy nie będą takie same haha

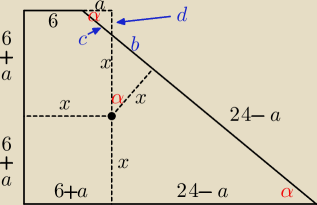wredulus_pospolitus: x = 6+a; z podobieństwa trójkątów:

c		24 + b + c − a		24 + b − a		x−d
	=		=		=
a		24		24 − a		x

d		2x		2x − d		b
	=		=		=
a		24		24−a		x

mamy 5 niewiadomych, więc z powyższych proporcji trza by było 4 równania ułożyć (bo jedno już mamy).

wredulus_pospolitus: I trzeba znowu poprawić rysunek, ponieważ mamy trójkąt gdzie przyprostokątna jest równa 'x', a przeciwprostokątna jest równa 'x−d'

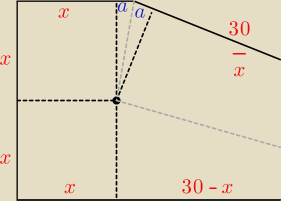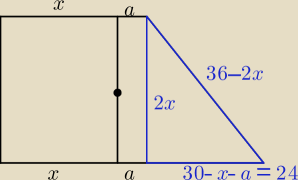
wredulus_pospolitus: a = 6 − x i to znowu mocno ułatwia bo mamy trójkąt prostokątny: '30−x , 2x , 36−2x' Pitagoras i masz 'x' ... masz wysokość podstawy ... to znowu trójkąt z wysokością ostrosłupa ... masz wysokość ostrosłupa. I wzór na objętość.

abcd: a skąd wiemy, że na tej przeciwprostokątnej jest a i 30/x?

abcd: i też trochę nie wiem skad się wziął ten pitagoras, a dokładnie 36−2x

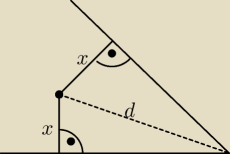wredulus_pospolitus: nie 30/x tylko 30−x z podobieństwa trójkątów, te dwa trójkąty są przystające (cecha BKB) Stąd wiemy, że trzeci ich bok jest taki sam. Skoro dolna podstawa jest równa 30, 'odcieliśmy' x ... to część 'trójkątna' to 30−x, więc i taka sama długość przechodzi na część ramienia. Analogicznie, druga część ramienia jest równa 'a' a wiemy, że a = 6 − x Stąd długość ramienia = 30−x + 6−x = 36 − 2x Zgadzamy się

wredulus_pospolitus: Stąd masz pitagorasa (pośpieszyłem się z jedną przyprostokątną, w efekcie jest jeszcze porściej) ... UWAGA powyższy rysunek absolutnie NIE jest w skali

abcd: aaa już rozumiem, dzieki

abcd: i wtedy w tym ostrosłupie każda krawedz boczna tez jest równa, prawda? bo są równe te odległości od spodka i byłyby równe krawędzie

wredulus_pospolitus: niee ... nie wszystkie są sobie równe ... te dwie idące od kątów prostych tak, pozostałe dwie są różne ... gdyby wszystkie były sobie równe to musiało by zachodzić: x = a = 30−x a to nie ma możliwości zajścia. Równe krawędzie i wysokości ścian bocznych masz jedynie w ostrosłupach prawidłowych, bo wtedy spodek wierzchołka tegoż ostrosłupa ląduje w punkcie który jest jednocześnie środkiem okręgu opisanego jak i okręgu wpisanego w podstawę (np. przecięcie przekątnych w kwadracie). Jako, że tutaj masz trapez prostokątny, to niemożliwe jest, aby na nim opisać okrąg (nie spełnia na to warunku) ... związku z tym, niemożliwe jest uzyskanie takiego ostrosłupa o takiej podstawie, tak aby jest krawędzie boczne były sobie równe.

abcd: ok dzieki

Iryt: Uciekł mi zapis i rysunek. Napisz abcd jakie masz wyniki.

Iryt: abcd , w razie trudności pisz to jeszcze raz narysuję i podam zapis.

abcd: wyszła mi objętość 600 i zgodziło się z odpowiedziami, więc chyba jest git

ax: Mnie objętość wyszła: V= 600

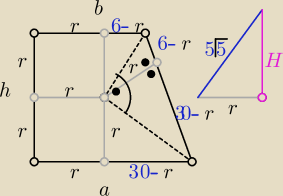Eta: r²=(6−r)(30−r) ⇒ r= 5 , 2r= h

	6+30
Pp=		*10
	2

P_p= 180 H²=(5√5)²−5² H=10 V= 600 =======