Ostrosłup plaszczyznaplaszczyzna Karolina : Dany jest ostrosłup prawidłowy czworokątny ABCDS o podstawie ABCD i krawędzi podstawy równej a. Krawędź boczna ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem 60°. Ostrosłup przecięto płaszczyzną przechodzącą przez punkt B, równoległą do prostej AC i nachyloną do podstawy pod kątem 30°. Oblicz pole przekroju. Dla mnie to jest trochę dziwne ze ma przechodzić przez punkt B i jednocześnie być równoległa do AC, bowtedy chyba jedyny jej punkt wspolny z ostrosłupem to B, więc to nie byłby przekrój. Byłoby milo, gdyby ktoś przynajmniej mógł mi narysować rysunek do tego zadania, bo nie wiem jak to narysować. Z góry dzięki

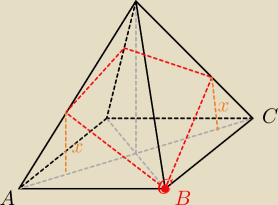
wredulus_pospolitus: Chodzi o taki przekrój, a ten przekrój będzie deltoidem.

Karolina : dziękuję bardzo

wredulus_pospolitus: kwestia równoległości względem AC wskazuje nam, że te wysokości w punktach na krawędziach AS i CS będa równe (dlatego zaznaczyłem obie jako 'x')

Karolina : a czy wtedy te odcinki x będą połową wysokości ostrosłupa? tak mi wyszło, ale wtedy nie zgodziła mi się odpowiedź

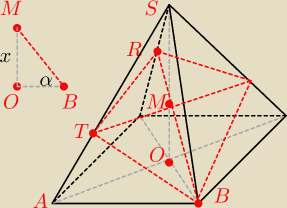
wredulus_pospolitus: niee ... nie będą ... ale wiesz, że ten deltoid jest pod kątem 30^o i możesz zbudować trójkąt prostokątny, Jedna przyprostokątna = |BO| (O −−− przecięcie przekątnych podstawy), druga będzie równa 'x'. Natomiast przeciwprostokątna będzie równa |BM| gdzie M to przecięcie przekątnych deltoidu. Mając już 'x' ... możesz z podobieństwa trójkątów ΔSMT i ΔSOA wyznaczyć |TM|. I jedyne co pozostanie do wyznaczenia to |RM|, a tak naprawdę to łatwiej będzie wyznaczyć |RB|, ponieważ wystarczy zauważyć, że w ΔBDR mamy: ∡DBR = 30^o, a ∡DRB = 60^o, w efekcie tenże trójkąt jest ... znamy |BD|, więc |RB| =

wredulus_pospolitus: I po to była nam potrzebna równoległość przekroju z AC ... aby |MO| = x i mieć podobieństwo trójkątów ΔSMT z ΔSOA.

Karolina : skala wyszła mi 3, wtedy x wychodzi a √6/6, wtedy przekątne to a √6/2 oraz a√2/3, ale wtedy pole wychodzi mi a² √3/6, a miało być a² √6/6

wredulus_pospolitus: no to sprawdzamy:

	hostrosłupa		√6
1. tg60o =		−−> hostrosłupa =		a
	√2a/2		2

	x		√6		1
2. tg 30o =		−−−> x =		a =		h
	√2a/2		6		3

	h−x		|TM|		2	√2		√2
3. z proporcji:		=		−−> |TM| =			a =		a
	h		√2a/2		3	2		3

	2√2
−−−> przekątna deltoidu = 2*|TM| =		a
	3

	|BR|		√6
4. cos30o =		−−−> |BR| =		a
	√2a		2

	1		√6		2√2		√3
5. P =		*		a*		a =		a2
	2		2		3		3

Nie wiem czemu w odpowiedzi jest wartość podzielona przez √2.

wredulus_pospolitus: Ja osobiście bym optował za taką właśnie odpowiedzią. Nie widzę nigdzie błędu w obliczeniach, może Ty coś zauważyć.

Karolina : teraz mi wyszło tak samo, jak tobie. Widocznie w odpowiedzi jest pomyłka. Bardzo dziękuję za pomoc