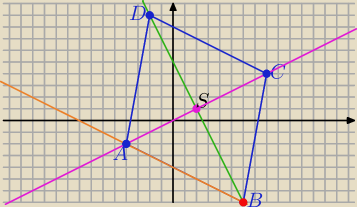
Geometria anya: Dany jest romb ABCD, którego środkiem symetrii jest punkt S= (2,1). Bok AB tego rombu leży na prostej o równaniu y = − 1/2 x − 4 oraz wektor AC = [12, 6]. Oblicz współrzędne wierzchołka B. Nie wiem co robię źle: 1. Uzależniłam współrzędne c od współrzędnych a (wykorzystując podany wektor) 2. Punkt (2,1) obrałam jako środek prostej AC i wyliczyłam współrzędne A i C używając wzoru na środek prostej. 3. Wyznaczyłam prostą AC 4. Przekątne rombu są prostopadłe, więc wyznaczyłam prostą DB używając twierdzenia o prostych prostopadłych i współrzędnych środka S 5. I stworzyłam układ równań DB z AB Niestety nie wychodzi mi wynik, co powinnam zrobić inaczej? Albo czy mam dobre myślenie i najprawdopodobniej błąd jest jednak w obliczeniach

Aruseq: Kolejne kroki są okej

anya: Czyli szukać błędu w obliczeniach?

Aruseq: Raczej tak. Wypisz tu kolejne wyniki, to rzucę okiem

Eta: → → AC=[12,6] to AS= [6,3] A=(2−6,1−3)=(−4,−2) i B=(2+6,1+3)=(8,4)

	6		1
aAC=		=		to aBD= −2
	12		2

BD: y= −2(x−2)+1 BD: y= −2x+5

	⎧	y= −2x+5
B:	⎩	y= −0,5x−4

−2x+5= −0,5x−4 ⇒ x=6 , y= −7 B=(6,−7) to D=(−2,9)