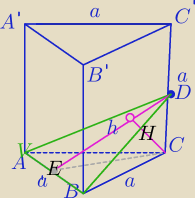
oblicz wysokość graniastosłup teke: Dany jest graniastosłup prawidłowy trójkątny ABCA'B'C', którego krawędź boczna jest równa krawędzi podstawy i ma długość a. Graniastosłup przecięto płaszczyzną przechodzącą przez punkty A ii B oraz punt D będący środkiem krawędzi bocznej CC'. Wyznacz wysokość ostrosłupa ABCD opuszczoną z wierzchołka C na podstawę ABD.

teke: proszę chociaż o podpowiedź, nie wiem jak policzyć na jakie odcinki wysokość dzieli wysokość trójkąta, bo chyba byłby promien gdyby krawedzie byly te same ale nie są

w:

	a√3
d=
	4

teke: no tyle to wiem, ale jakiś sposób jak zrobić by się przydał

Mila:

	1		1
VABCD=		*PΔABC*CD=		*PΔABD*H
	3		3

1)

	1		a2√3		a		a3√3
VABCD=		*		*		=
	3		4		2		24

2) W ΔDCE:

	a√3		a		3a2		a2
h2=(		)2+(		)2=		+		=a2
	2		2		4		4

h=a ==

	a3√3		1		1
3)		=		*(		a2)*H
	24		3		2

	a*√3
H=
	4

====== II sposób ( jeśli zauważysz jakim Δ jest Δ ECD)