Parametr Kuba : No jakich wartości parametru M równanie x²−(m−1)x+2m−5=0 ma dwa rozwiązania rzeczywiste z których jedna jest dodatni a drugie mniejsze od − jedynki? Jakie założenia do tego i dlaczego?

chichi: zdefiniujmy f(x) = x² − (m − 1)x + 2m − 5. wiemy, że wykresem tej funkcji jest parabola o ramionach skierowanych ku górze, zatem "lewą gałąź" trzeba wypchnąć na prawo od (−1) czyli f(−1) < 0, a tę "prawą gałąź" na prawo od 0, czyli f(0) < 0, więcej nie trzeba bo jeśli parabola zjechała poniżej osi OX i ma ramiona skierowane ku górze, to na pewno ma dwa rozwiązania

chichi: na lewo od (−1) **

chichi:

Kuba : Dzięki

Kuba : A czemu właśnie jak jedziemy w prawo od zera to f(0) nie jest większe od 0?

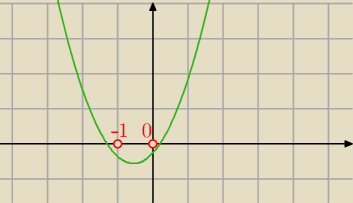
chichi: no to spójrz na wykres

Kuba : No właśnie patrzę i wydaje mi się ze są dodatnie te wartości po tej stronie; nigdy nie byłem asem z matmy i ten parametr to jest tragedia

wredulus_pospolitus: f(x) = x²−(m−1)x+2m−5 1. Współczynnik kierunkowy (wartość przy najwyższej potędze) jest większy od 0 (a = 1) 2. Związku z tym ramiona paraboli będą skierowane do góry. 3. Związku z tym, aby jedno miejsce zerowe było >0 a drugie <−1 to musi zajść: I. f(−1) < 0 (co oznacza, że jedno miejsce zerowe jest < −1 ; a drugie > −1) II. f(0) < 0 (co oznacza, że jedno miejsce zerowe jest < 0 ; a drugie > 0) w efekcie otrzymujemy −> jedno miejsce zerowe < −1 , a drugie > 0

Jolanta: Pytają o parametr m Trzeba chyba zacząc od Δ Skoro mają byc dwa pierwiastki Δ>0

wredulus_pospolitus: Δ nie trzeba liczyć ... jeżeli słabszy warunek niż ten co stawiamy, czyli : f(−1) < 0 ∨ f(0) < 0 załatwia nam kwestię Δ>0 (bo trudno, że Δ≤0 a jednocześnie funkcja przyjmowała wartości mniejsze od zera, jeżeli a=1)

wredulus_pospolitus: bo trudno, aby*

Jolanta: Niestety za trudne

Jolanta: f(−1)<0. i f(0)<0 (−1)²+m−1+2m−5<0. 2m−5<0 3m<5. m<2,5

	5
m<
	3

m∊(−∞,5/3) Dobrze?