Stereometria anya: Dany jest ostrosłup prawidłowy trójkątny ABCDEF, którego objętość jest równa 9. Płaszczyzna przechodząca przez krawędź AB i zawierająca środek ciężkości podstawy DEF jest nachylona do płaszczyzny podstawy pod kątem α takim, że tgα= 9/8. Oblicz pole przekroju graniastosłupa tą płaszczyzną.

wredulus_pospolitus: okey i teraz: 1. Czy został zrobiony rysunek? 2. Czy wiesz gdzie dokładnie leży środek ciężkości trójkąta równobocznego DEF ? Jeżeli tak ... to gdzie napotykasz na problem

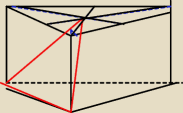
anya: Środek ciężkości to miejsce przecięcia środkowych, a mniej więcej tak wygląda mój rysunek. Problem polega na tym, że nie wiem co zrobić dalej

.: 1. Przekrój nie jest trójkątem a trapezie rownoramiennym 2. Środek ciężkości w trójkącie równobocznym jest tam gdzie środek okręgów wpisany/opisany, czyli w 1/3 do 2/3 wysokości trojkata. 3. Korzystając z tangensa możesz wyrazić wysokość ostrosłupa od wysokości podstawy, a w konsekwencji od boku trójkąta 4. W efekcie masz objętość wyrażona jako wartość zależna od zmiennej 'a' (bok trójkąta), stąd masz bok a 5. Wyracasz do przekroju, z chociażby Tw. Pitagorasa możesz policzyć wysokosc trapezu, a górna podstawa z chociażby proporcji. Niestety, obecnie jestem 'wyjechany' więc rysunków robić nie będę.

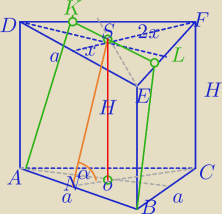
Mila: V=9 |NC|=h

	a√3		1		a√3		a√3
1) h=		, |ON|=		*		=
	2		3		2		6

	H		9
tgα=		=
	|ON|		8

	9		a√3
H=		*
	8		6

	3a√3
H=
	16

2)

	a2√3
V=		*H
	4

a2√3		3a√3
	*		=9 stąd obliczysz a
4		16

3) dokończ

anya: Bardzo dziękuję

anya: A jeszcze pytanie, czemu trapez jest przekrojem?

Mila: Spróbuj wyobrazić sobie , że odcinasz jednym cięciem kawałek ciastka szerokim nożem. Czy to możliwe jak na rys. 17: 20 ?

anya: Nie jest to możliwe, dzięki za wytłumaczenie

Mila: