geometria analityczna równoramienny proste Karolina: Ramiona trójkąta równoramiennego zawierają się w prostych x + 7y + 16 − 0 oraz x − y − 1 = 0. Prosta k zawiera podstawę tego trójkąta i przechodzi przez punkt P = (2, 0). Napisz równanie prostej k. Baaardzo proszę o pomoc

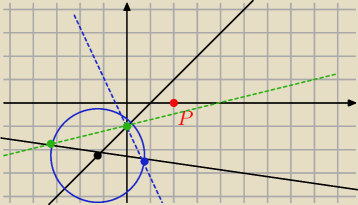
wredulus_pospolitus: Moja sugestia (zapewne zamysł układającego był inny): 0. Robimy rysunek poglądowy 1. Wyznaczamy punkt przecięcia się tych prostych (mamy wierzchołek trójkąta, powiedzmy C). 2. Piszemy wzór okręgu o jakimś promieniu (powiedzmy r = 1). 3. Sprawdzamy jakie współrzędne mają punkty na prostych, w których ów proste przecinają okręg. 4. Wybieramy dwa zestawy po 2 punkty (po jednym dla każdej prostej − patrz przykładowy wybór niebieskie i zielone) I wyznaczamy proste przechodzące przez dane 2 punkty. 5. Szukana prosta k będzie prostą RÓWNOLEGŁĄ do tych prostych (dwa przypadki), więc wyznaczasz równoległą do posiadanej prostej, ale taką aby przechodziła przez punkt P. Koooniec

Karolina: spróbuję tak, dzieki

wredulus_pospolitus: Zauważ, że punkty przecięcia okręgu z prostymi są równoodległe od środka okręgu = wierzchołka trójkąta. Dzięki temu uzyskujemy prostą która zawiera podstawę trójkąta równoramiennego ... Przesunięcie (zapisanie równoległej do tejże prostej) do punktu P ma na celu po prostu wyznaczenie takiej prostej o którą pytają w zadaniu. Tylko tak jak napisałem wcześniej −−− będą dwie opcje (równoległa do zielonej i równoległa do niebieskiej)

Karolina : faktycznie chyba tak wychodzi

wredulus_pospolitus: Alternatywną wersją (o którą zapewne chodziło autorowi zadania) jest: 1. Wyznaczamy równanie dwusiecznej kątów pomiędzy danymi nam prostymi (https://tomaszgrebski.pl/video-lekcje?view=article&id=550&catid=44) 2. Wyznaczamy PROSTOPADŁE do tych dwusiecznych, przechodzące przez punkt P. Jak widzisz ... będzie 'szybciej' o ile tylko kojarzysz w jaki sposób zrobić punkt 1

Karolina: o super, pzyda się, dziękuję

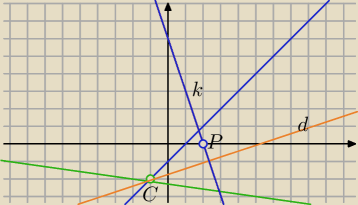
Mila: II sposób z równaniem dwusiecznej (z 8: 50 wredulus spać nie może− ranny ptaszek) d− zawiera dwusieczną k⊥d , P∊k

wredulus_pospolitus: @Miluś −−− dwie dwusieczne mają być

Mila: To już zostawiłam dla Karolinki

Mila: x + 7y + 16 = 0 oraz x − y − 1 = 0. Dwusieczne:

|x+7y+16|		|x−y−1|
	=
√50		√2

Wika: bardzo wam dziękuję udało mi się zrobić, wyszło 3x+y−6 = 0 lub x−3y−2=0