Parametr Kuba : Znajdź wszystkie wartości parametru a dla których podane nierówność jest prawdziwa dla wszystkich liczb rzeczywistych (4−a²)x²−2(a−2)x+1>0. Czy ktoś mógłby mi wytłumaczyć dlaczego tutaj niby delta ma być mniejsza od zera a nie większa od 0? Proszę tak krok po kroku.

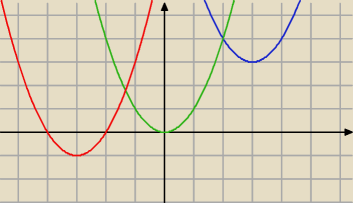
wredulus_pospolitus: NIBY dlatego, aby wtedy nie było miejsc zerowych, czyli aby wtedy cały wykres paraboli mieścił się powyżej osi OX. Tutaj masz przykład funkcji dla których równanie wielomianowe ma: Δ>0 czyli funkcja przyjmuje zarówno dodatnie jak i ujemne wartości Δ=0 czyli funkcja przyjmuje nieujemne wartości Δ<0 czyli funkcja przyjmuje tylko dodatnie wartości

Kuba : Dzięki a czemu jak napisze że 4−a² jest większe od 0 to później przedziały od −2 do 2 są domknięte zamiast otwarte?

wredulus_pospolitus: Nie wiem czemu, jasnowidzem nie jestem. Winny być takie przypadki: 1. (4−a²) > 0 ; Δ < 0 (parabola powyżej osi OX) 2. (4−a²) = 0 ; (a−2) = 0 ; 1 > 0 (funkcja stała powyżej osi OX)

Kuba : A no dobra bo ja zrobiłem tak że 4−a²>0 i z tego mi wyszło a<2 lub a>−2 i zastanawia mnie tylko czemu a należy do przedziału od <−2,2> domkniętych

chichi: bo a = ±2 sprawdzasz osobno... nikt nie mówi, że ta nierówność musi być kwadratowa, a jedynie spełniona dla kazdego x rzeczywistego

Kuba : Dzięki