Planimetria :): Dany jest czworokąt ABCD, w który wpisano okrąg. Punkty E, F, G, H są punktami styczności tego okręgu z bokami czworokąta ABCD oraz |<HAE| = α, |<EBF| =β Wykaż, że miara <FFG czworokąta EFGH jest równa 1/2 * (360° − α − β)

wredulus_pospolitus: Masz do tego rysunek? Jak się mają punkty E,F,G,H względem A,B,C,D W sensie ... na jakich bokach są te punkty miara kąta FFG

:): Właśnie nie ma tego podane i nie wiem

:): Tylko to polecenie było

Mefistofeles: Niech punktyEFGH leżą odpowiednio na bokach AB,BC,CD,DA Ale nie może byc kąt FFG i o to chodzi . Może ma być kąt EFG?

:): O faktycznie, mój błąd. Chodzi o kąt FGH

:): Ma ktoś pomysł jak to zrobić?

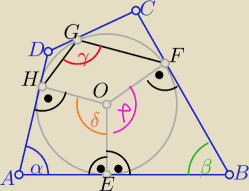
Eta: δ= 180^o−α φ= 180^o−β δ+φ= 360 −α−β kat γ −− wpisany oparty na łuku HEF kąt δ+φ −− środkowy oparty na tym samym łuku HEF zatem mamy tezę:

	1
γ=		(360o−α−β)
	2

================= c.n.w.