trójkąt
Amelia: W trójkącie ABC dane są AB = 10 , ∘ ∡A = 30 i ∘ ∡B = 45 . Oblicz długości pozostałych boków
tego trójkąta i promień okręgu opisanego na tym trójkącie.
19 kwi 14:52
wredulus_pospolitus:
| | a | | b | | c | |
musisz skorzystać z tw. sinusów: R = |
| = |
| = |
| |
| | 2sinα | | 2sinβ | | 2sinγ | |
zauważ także, że: 180 − 30 − 45 = 105 = 90 + 45
więc sin105
o = sin(90
o + 45
o) = .... 45
o 
19 kwi 14:57
wredulus_pospolitus:
gdzie α,β,γ to kąty na przeciwko boków (odpowiednio) a,b,c.
19 kwi 14:58
Eta:
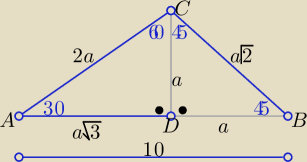
Taki trójkąt składa się z dwóch "sklejonych" trójkątów :ekierkowych"
zatem |AB|= a
√3+a}= 10⇒ a(
√3+1)=10 ⇒ a= 5(
√3−1)
to |AC|=2a=10(
√3−1) i |BC|= a
√3= 5
√3(
√3−1)
=======================================
i po ptokach
19 kwi 16:11