Wykaż, że pole Olek4872: W prostokącie ABCD dane są: |AB|=a, |BC|=b i a>b. Okrąg o średnicy AD przecina przekątną BD prostokąta w punkcie E.

	ab3
Wykaż, że pole trójkąta AED jest równe		.
	2(a2+b2)

Zapisz obliczenia.

wredulus_pospolitus: Jak AD może przecinać BD

Olek4872: Chyba coś takiego.

wredulus_pospolitus: dobra ... źle przeczytałem Zauważ, że Trójkąt AED jest trójkątem prostokątnym. z podobieństwa trójkątów mamy:

a		|AE|		a
	=		−−−> |AE| =		|ED|
b		|ED|		b

z tw. Pitagorasa mamy |AE|² = b² − |ED|²

	b2+a2		b4
co po podstawieniu da nam: |ED|2*		= b2 −−−> |ED|2 =
	b2		b2+a2

i przechodzimy do pola

	|AE|*|ED|		a		a		b4		ab3
PΔ =		=		|ED|2 =		*		=
	2		2b		2b		b2+a2		2(a2+b2)

wredulus_pospolitus: Polecam: 1. Zastanowić się skąd wiem że ΔAED jest prostokątny 2. Z jakiej cechy skorzystałem w celu uzasadnienia dlaczego AED jest podobny do ABD 3. Zauważ małe 'skróty myślowe' przy przekształceniach.

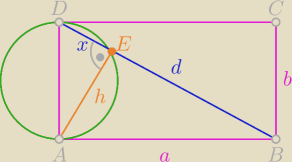
chichi: niech d = |BD|, |DE| = x.

	1		1		ab
d = √a2 + b2, PΔABD =		ab =		hd ⇒ h =
	2		2		√a2 + b2

	a2b2		b2
h2 + x2 = b2 ⇔ x2 = b2 −		⇔ x =
	a2 + b2		√a2 + b2

	1		1	b2	ab		ab3
PΔAED =		xh =				=
	2		2	√a2 + b2	√a2 + b2		2(a2 + b2)

□