zmienna ciagla łubudubu: mam takie zadanie https://ibb.co/8N5Yz1b zrobilem funkcje gestosci 0 x<−1 f(X) 1 −1≤x≤0 0 x>0 0 y<2 f(y) 1/2 −2≤y≤4 0 y>4 i nie wiem co dalej

wredulus_pospolitus: yyyy nieee

	⎧	0 gdy x<−1
	⎜	1/3 gdy x∊[−1;0)
f(x) =	⎨	0 gdy x∊[0;2)
	⎜	1/3 gdy x∊[2;4)
	⎩	0gdy x≥4

wredulus_pospolitus: I niby dlaczego zmienna losowa ma być ciągła

łubudubu: w sensie nie ciagla tylko zmienna rozklad jednostajny

łubudubu: no to wzialem z tych wzorow typu ze f(x) = 1/(b−a) <a ; b> 0 x rozne od <a ;b>

wredulus_pospolitus: fajne ... tylko tutaj zmienna losowa X ma rozkład jednostajny na przedziale [−1;0] u [2;4] a nie ... [−1,0] a inna zmienna losowa na przedziale [2;4]

łubudubu: a skad wziales te liczby w twojej funkcji

wredulus_pospolitus:

	1
przedział ma długość 3 ... więc zmienna przyjmuje prawdopodobieństwo
	3

łubudubu: coo

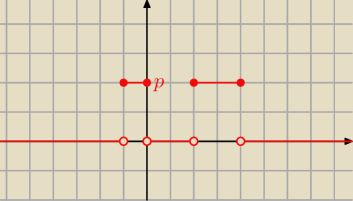
wredulus_pospolitus: tak wygląda wykres funkcji gęstości dla zmiennej losowej X. nie znamy 'p' ale wiemy że obszar pomiędzy funkcją a osią OX jest równy '1'.

	1
związku z tym: p*|0 − (−1)| + p*|4−2| = p + 2p =1 −−> p =
	3

łubudubu: a to w takim razie czy od [2 ; 4] nie bedzie 2/3?

wredulus_pospolitus:

	1
Gdyby był TYLKO przedział [2,4] (a w pozostałych 0) to wtedy p =		na tym przedziale.
	2

Nie rozumiesz −−− całka z gęstości ma być równa 1 ... nie mniej ... nie więcej ... dokładnie 1 jeżeli p = 2/3 na przedziale [2;4] to całka z tego obszaru równa jest 4/3 > 1

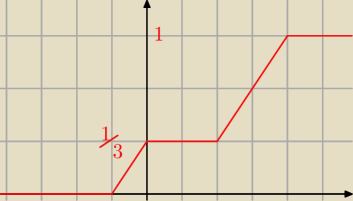
wredulus_pospolitus: tu masz wykres dystrybuanty zmiennej losowej X

łubudubu: a bo to jest tak ze jak calka z funkcji gestosci musi byc rowna jeden to znaczy ze pole wykresu jest rowne jeden wiec tam po lewej mnoze 1 * 1/3 a po prawej 2* 1/3 i dlatego 1

wredulus_pospolitus: tak ... całka z całej dziedziny ( czyli od −∞ do ∞) ma być równa 1. Jako, że rozkład masz jednostajny na danym przedziale ... to prawdopodobieństwo na nim będzie stałe, więc funkcja gęstości na tym przyjmie stałą wartość ... łączna długość przedziału równa jest '3' ... więc prawopodobieństwo (wartość funkcji) musi się równać 1/3 ... tak aby 3* ¹/₃ = 1

łubudubu: czyli teraz dystrybuante z calki i policzyc to P i gotowe

wredulus_pospolitus: tak ... wykres dystrybuanty Ci nawet narysowałem