Optymalizacja
koks2: Dany jest trapez równoramienny. Przekątna tego trapezu ma długość 120. Oblicz jakie jest
największe pole powierzchni tego trapezu
16 kwi 14:54
wredulus_pospolitus:
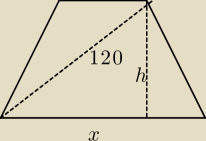
Treść zadania sugeruje, że obie przekątne są sobie równe (co nie musi mieć miejsca w trapezie
równoramiennym, o czym niestety autor zadania zapomniał).
Zauważmy, że P
trapezu = x*h
a z tw. Pitagorasa: h
2 = 120
2 − x
2 −> h =
√1202 − x2
więc P(x) = x*
√1202 − x2
pochodna ... szukasz maksimum
16 kwi 15:08
koks2: czemu polem trapezu jest iloczyn podstawy z wysokoscia, a nie uzywamy wzoru 1/2(a+b)h?
16 kwi 18:47
koks2: dobra juz wiem
1/2*2ah to da ah
16 kwi 18:52
koks2: nie dobra jednak nie
dalej nie wiem skad

16 kwi 18:55
Aruseq: Bo x to nie dłuższa podstawa, a ta jej dłuższa część po lewej stronie
16 kwi 18:56
koks2: no tak, ale nie wiem skad to sie wzielo i nie wiem jak to sobie wytlumaczyc xd
16 kwi 19:07
ABC:
bo x=(a+b)/2 proste rachunki
16 kwi 19:22
Jolanta: Po lewej stronie masz trójkąt .Wyobraź sobie,że go odcinasz i montujesz z lewej strony ale
podstawą do góry Otrzymasz prostokąt o bokach x i h
16 kwi 19:48
koks2: o, dzieki ABC, wlasnie tego klocka brakowalo do calosci XD
16 kwi 19:57
 Treść zadania sugeruje, że obie przekątne są sobie równe (co nie musi mieć miejsca w trapezie
równoramiennym, o czym niestety autor zadania zapomniał).
Zauważmy, że Ptrapezu = x*h
a z tw. Pitagorasa: h2 = 1202 − x2 −> h = √1202 − x2
więc P(x) = x*√1202 − x2
pochodna ... szukasz maksimum
Treść zadania sugeruje, że obie przekątne są sobie równe (co nie musi mieć miejsca w trapezie
równoramiennym, o czym niestety autor zadania zapomniał).
Zauważmy, że Ptrapezu = x*h
a z tw. Pitagorasa: h2 = 1202 − x2 −> h = √1202 − x2
więc P(x) = x*√1202 − x2
pochodna ... szukasz maksimum
