stereometria eee: podstawą graniastosłupa prostego jest romb o kącie ostrym α. krótsza przekątna graniastosłupa ma długość 1 i tworzy ze ścianą boczną kąt β. oblicz pole powierzchni bocznej tego graniastosłupa. Prosze o rysunek i rozwiazania bo totalnie nie umiem sie za to zabrac. Odp ma wyjsc = ^{4 sinβ √sin2 α− 2sin2 β (1−cosα)} _{sin² α}

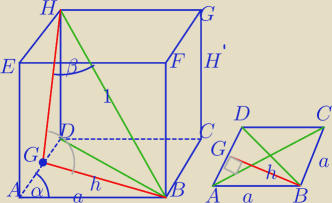
Iryt: G − rzut prostokątny punktu B na pł. ADHE GB⊥AD 1) W ΔAGB:

	h		h
sinα=		, a=
	a		sinα

W ΔHGB: |∡HGB|=90^o

	h
sinβ=		, h=sinβ
	1

	sinβ
a=
	sinα

============ 2) H'−Wysokość graniastosłupa: W ΔBAD: |DB|²=a²+a²−2a² cosα=2a²−2a²cosα W ΔHDB: |DB|²+H'²=1

	sin2β		sin2β
H'2=1−2a2+2a2 cosα=1−2		+2*		*cosα=
	sin2α		sin2α

	sin2α−2sin2β+2 sin2β*cosα
=
	sin2α

	√sin2α−2sin2β(1−cosα)
H'=
	sinα

	4 sinβ√sin2α−2sin2β(1−cosα)
Pb=
	sin2α

============================