W trójkącie równobocznym ABC Lutek:

	1
W trójkącie równobocznym ABC na boku BC wybrano punkt D taki,że |BD|=		|DC|
	3

Wyznacz sinus kąta CAD

.: Zwiazku z jakim działem konkretnie to zadanie jest? Kielismy Tw. cosinusów?

.: Mielismy*

Lutek: Tak

wredulus_pospolitus: To w takim razie moja propozycja jest następująca:

	1
1. zauważamy, że |BD| =		|BC|
	4

2. oznaczmy |AB| = 4x (wtedy |BD| = x) 3. z tw. cosinusów: |AD|² = 16x² + x² − 2*4x*x*cos60^o |AD|² = 17x² − 4x² = 13x² −−−> |AD| = √13x

	1
4. z proporcji (1) wiemy, że hABD =		hABC
	4

	1
więc także PABD =		PABC
	4

	3		3		(4x)2√3
więc, PADC =		PABC =		*		= 3√3x2
	4		4		4

	|AD|*h		√13x
PADC =		=		*h
	2		2

	√13x		6√3		6√39
więc:		*h = 3√3x2 −−−> h =		x =		x
	2		√13		13

5.

	h		6√39x		3√39
sin(∡CAD) =		=		=
	|AC|		13*4x		26

chyba nigdzie nie zrobiłem babola

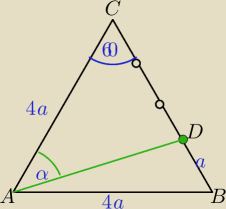Iryt: |AD|=√13a ( j.w obliczył kolega 2) W ΔADC:

3a		a√13
	=
sinα		sin60o

stąd

	3√39
sinα=
	26

=============

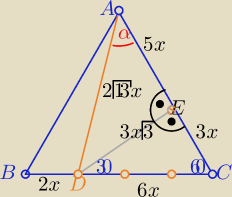Eta: ΔDCE "ekierkowy" oznaczenia na rys.

	3x√3
sinα=
	2√13x

	3√39
sinα=
	26

=============