Oblicz obwód czworokąta ABCD. kuba: W okrąg o promieniu długości √5 jest wpisany czworokąt ABCD, w którym |AB|=|AD|, miara kąta BCD jest równa 120° i stosunek pola trójkąta ABC do pola trójkąta ACD wynosi 1/3. Oblicz obwód czworokąta ABCD.

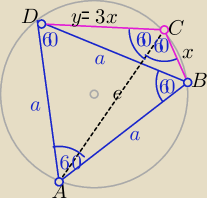
Eta: 1/ z warunku wpisania czworokąta w okrąg |∡A|=180^o−120^o= 60^o to ΔABD równoboczny

	a√3
R= √5=		⇒ a= √15
	3

2 / P_ABC=P₁ P_ACD= P₂

	P1		1		e*x*sin60o/2
		=		=
	P2		3		e*y*sin60o/2

to y= 3x 3/ z tw. cosinusów w ΔBCD a²= 9x²+x²+2*3x*x*(1/2) dokończ Obwód (ABCD) : L= 2a+4x=..........