Punkty wewnętrzne trójkąta Maja: Przez punkt wewnętrzny P trójkąta ABC poprowadzono proste równoległe do wszystkich boków. Wycięły one trzy trójkąty o polach Q, R, T. S jest polem trójkąta ABC.Udowodnij, że √S=√Q+√R+√T.

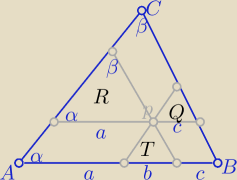
Eta: trójkąty o polach R,Q,T są podobne do trójkąta ABC z cechy (kkk) to stosunek pól jest równy kwadratowi skali podobieństwa

√R

a

√Q

c

√T

b

=

i

=

i

=

√S

a+b+c

√S

a+b+c

√S

a+b+c

dodając stronami te trzy równości i mnożąc przez √S otrzymasz tezę

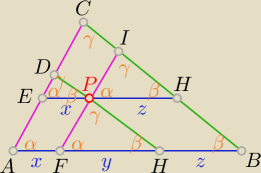chichi: ΔFHP ~ ΔPHI ~ ΔEPD ~ ΔABC (cecha k−k−k), niech P_ΔFHP = Q, P_ΔPHI = R, P_ΔEPD = T,

	y		√Q
(1)		=
	x + y + z		√S

	z		√R
(2)		=
	x + y + z		√S

	x		√T
(3)		=
	x + y + z		√S

dodając stronami mamy, że:

x + y + z		√Q + √R + √T
	=		⇔ √S = √Q + √R + √T □
x + y + z		√S

chichi: @Eta

Maja: Dziękuuuuję ♥♥

Eta: Na zdrowie