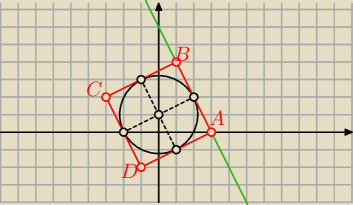
analityczna eee: W prostej o równaniu 2x+y−6=0 zawiera się bok kwadratu opisanego na okręgu o równaniu x²+ y² −2y −4=0. Wyznacz wspolrzedne wierzcholkow tego kwadratu. Probowalem to zrobic i policzylem rownanie okregu oraz punkt stycznosci okregu z prosta ale nie wiem co dalej. kombinowalem z wektorami ale wole na nich nie rozwiazywac,jakies ktos ma pomysl na rozpisanie tego?

wredulus_pospolitus: od punktu styczności odkładasz 'odległość środka okręgu od prostej = promień okręgu' i masz współrzędne wierzchołków kwadratu na prostej. Ja je odłożyć? To już od Ciebie zależy, ja osobiście bym zrobił wzorem okręgu o środku = punkt styczności, promień = promień pierwotnego okręgu)

wredulus_pospolitus: pozostałe dwa wierzchołki, to na przykład: oznaczmy A i D jako wyznaczone wierzchołki, S środek okręgu o którym mowa w zadaniu. 1. − prosta przechodząca przez A i S − S jest środkiem odcinka AC −−−> wyznaczasz C − analogicznie dla prostej przechodzącej D i S 2. − prostopadła do podanej w zadaniu przechodząca przez A − prostopadła do podanej w zadaniu przechodząca przez D − równoległa do podanej w zadaniu, odległa o 2r (tak aby była styczna do okręgu) − przecięcia prostych wyznaczają współrzędne oczywiście to nie jedyne sposoby

aa: