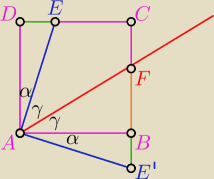
 odkładamy ΔADE na boku AB i dalej:
|∡DEA| = 90o − α ⇒ |∡AEC| = 90o + α
|∡CFA| = 360o − 90o − 90o − α − γ = 180o − α − γ ⇒ |∡AFE'| = α + γ
zatem ΔAE'F − równoramienny, stąd |AE'| = |BE'| + |BF| = |BF| + |DE| □
odkładamy ΔADE na boku AB i dalej:
|∡DEA| = 90o − α ⇒ |∡AEC| = 90o + α
|∡CFA| = 360o − 90o − 90o − α − γ = 180o − α − γ ⇒ |∡AFE'| = α + γ
zatem ΔAE'F − równoramienny, stąd |AE'| = |BE'| + |BF| = |BF| + |DE| □ 
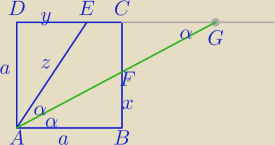 Tu rachunki:
1) ΔAEG −Δrównoramienny
|AE|=|EG|
|DG|=y+z
2)
ΔABF∼ΔADG
Tu rachunki:
1) ΔAEG −Δrównoramienny
|AE|=|EG|
|DG|=y+z
2)
ΔABF∼ΔADG
| x | a | ||
= | ⇔a2=x(y+z) | ||
| a | y+z |