wyznacz punkt d werdi: W układzie współrzędnych dane są punkty A = (−3 ,−3 ) , B = (9,1) i C = (8 ,−6 ) . Wyznacz wszystkie punkty D prostej AB , które są różne od punktów A i B , i dla których suma pól trójkątów ADC i BDC jest mniejsza od 120.

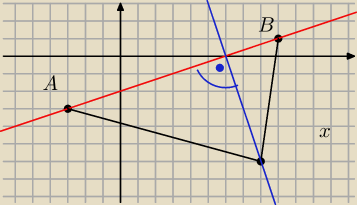
wredulus_pospolitus: 1. wyznaczamy prostą AB 2. wyznaczamy prostą prostopadłą przechodząc przez C i wyliczamy długość wysokości LUB ze wzoru na odległość punktu od prostej wyznaczamy tą wysokość 3. h = √40 = 4√10

	|AD| + |BD|
4. Zauważamy, że PΔADC + PΔBDC =		*4√10 < 120 −−−>
	2

−−−> |AD| + |BD| < 6√10 5. Jeżeli D leży na odcinku AB to |AD| + |BD| = |AB| = √16 + 144 = 4√10 6. Jeżeli D leży poza odcinkiem AB to |AD| + |BD| = 2*|AD| + 4√10 |AD| + |BD| = 2*|BD| + 4√10 (zależy po której stronie odcinka leży punkt D) 7. Więc |AD| < √10 lub D leży wewnątrz AB lub |BD| < √10 8. Wyznaczasz przedział jaki spełnia te warunki czyli punkty o współrzędnych (x ; x/3 − 2) gdzie x ∊ (−6 ; 12). UWAGA Z ostatecznego wyniku należy odrzucić współrzędne punktu A i B

wredulus_pospolitus: uuuu ... źle policzyłem wysokość popraw i skoryguj wynik