Proszę o pomoc to zadanie jest chore 😭😭😭 skibiditoaleta123: W okrąg o równaniu x² + y² − 12x − 8y + 32 = 0 wpisano trójkąt równoboczny ABC w którym A = (2,6). Oblicz współrzędne pozostałych wierzchołków trójkąta.

Little Mint: To zadanie nie jest chore Rzecz nr 1 potrafisz napisac równanie okregu w postaci kanonicznej ? jesli tak to napisz . Potem postaram sie pomóc

skibiditoaleta123: udalo mi sie juz rozwiazac, doszedlem do momentu gdy mialem a = 2√15 i wspolrzednie srodka, nie wiedzialem co dalej ale trzeba zrobic okrag wokol punktu a o promeniu 2√15

uczen201034: bardzo dziekuje za pomoc, czekałem na rozwiazanie tego zadania

.: skibi − jest to tylko jedna z możliwości. Można też bylo: 1. Wyznaczamy środek okręgu. 2. Wyznaczamy prosta przechodząca przez A i S. Sprawdzamy współrzędne przecięcia tej prostej z okregiem (nazwijmy to D) 3. Wyznaczamy środek odcinka SD. 4. Prowadzimy prostopadła do (2.) przez te że środek odcinka (4.) 5. Szukamy punktu przecięcia z okregiem − > to są nasze brakujące wierzcholki

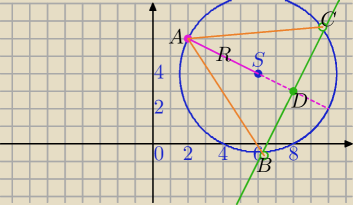
Iryt: 1) (x−6)²+(y−4)²=20 R=2√5 h_Δ=3√5 S=(6,4) A=(6,2) AS^→=[4,−2] S=(6,4)→T{[2,−1])⇒D=(8,3)− środek podstawy Δ 2)

	1
Prosta AS: y=−		x+7
	2

k: Prostopadła do AS i D=(8,3)∊k y=2x+b , 3=2*8+b, b=−13 y=2x−13 3) (x−6)²+(2x−13−4)²=20 x=8−√13 i y=2*(8−√13)−13=3−2√3 B=(8−√13 ,3−2√13) dokończ

k: skąd te √13 ? ?

Iryt: Równanie kwadratowe. Rozwiąż. To literówka , ma być: √3, raz się pomyliłam, a potem kopiowałam.