f gestosci ania: A. Czy można dobrać stałą c tak, aby funkcja 𝑓(𝑥) = { {0 dla |𝑥| ≥ 1 𝑐(𝑥² − 5) dla |𝑥| < 1 była funkcją gęstości zmiennej losowej X? Odpowiedź uzasadnij. Oblicz 𝐹(−0,5); 𝑃(0,5 < 𝑋 < 1,5). B. Dobierz stałe A i B tak, aby funkcja 𝐹(𝑥) = { 0 dla 𝑥 ≤ 0

	𝐵
𝐴 −		dla 𝑥 > 0
	1+𝑥2

była dystrybuantą zmiennej losowej X o rozkładzie ciągłym. Wyznacz funkcję gęstości oraz obliczyć 𝑃(0,5 < 𝑋 < 1,5); 𝐹(0,5).

wredulus_pospolitus: Czy wiesz jakie warunki musi spełnić funkcja, aby mogła uchodzić za funkcję gęstości zmiennej losowej To samo pytanie dotyczy dystrybuanty.

wredulus_pospolitus: czyli rozumiem, że po prostu czekasz na gotowca przed kołem ... tak

ania: czy w 1 nalezy jakos obliczyc calke tak zeby na przedziale suma byla 1?

wredulus_pospolitus: tak ... ∫^∞_∞ f(x) dx = 1

wredulus_pospolitus: miało być ∫^∞_−∞ f(x) dx = 1

ania: a dobra juz wiem

ania: moge potem wrzucic zdjecie rozwiazania zeby ktos rzucil okiem czy jest dobrze zapisane?

ania: bo zrobilam

wredulus_pospolitus: to wrzucaj na jakiś serwis i dawaj linka

ania: chwila tylko ladnie przepisze

ania: a czemu w A jak wychodzi mi ze c = −3/28 i wychodzi mi 0 dla (−∞ ; −1) −3/28 ((x³ /3 −5x) <−1 : 1> 0 x>1 i calka z tego obszaru wychodzi mi 0

wredulus_pospolitus: no to źle policzyłaś 'c'

wredulus_pospolitus: Jak Ci może później całka wychodzić 0 skoro dobrałaś tak parametr 'c' aby ta całka była równa 1

ania: ale powyzej jedynki jest juz 0 i ta dystrybuanta w nieskonczonosci nie bedzie wynosic 1

wredulus_pospolitus: heeee F(x) = ∫_−∞^x f(s) ds innymi słowy ... wartość dystrybuanty w punkcie x_o jest równa polu pod gęstością od −∞ do punktu x_o. Skoro 'cała powierzchnia' = 1 jest na przedziale [−1 ; 1] to wartość dystrybuanty dla każdego x_o ≥1 będzie równa '1' (bo 'żadna nowa powierzchnia nie przybywa')

ania: zaraz wysle zdjecie

Ania: https://ibb.co/2j7gxWy Czy w skrócie takie wyniki mają sens? Tam te przedziały to bym po.rpostu bym podstawiła z dystrybuanty

wredulus_pospolitus: dokładnie tak też trza zrobić

ania: a jak polaczylam dla <−1 ; 1> i mi wyszlo w dystrybuancie (jakby 2 razy wiecej dla tego przedzialu niz rozbiajac) −1/14 x³ + 15/14 x to moze byc tak? Bo jak bede liczyla F(−0.5) to wyjdzie inaczej niz na zdjeciu

Ania: https://ibb.co/ZzYvhzm

Ania: Bo zrobiłam tak nie rozdzielając tego przedziału i się zastanawiam czy jest ok wszystko. Bo zrobiłam tak jak na wykładzie podstawiając zmienna T I licząc dokładnie tak samo

wredulus_pospolitus: błędnie policzona całka nie −1/14 t³ tylko −1/28 t³ po drugie −−− po kiego grzyba znowu liczysz tą całkę

wredulus_pospolitus: tak samo nie 15/14 tylko 15/28

wredulus_pospolitus: i taka uwaga liczysz całkę: ∫^x₋₁ c(t²−5) dt = F(x) to co Ty liczysz wygląda tak: F(0.5) = ∫⁻¹_−∞ f(t) dt + ∫^0.5_−0.5 f(t) dt = ... a gdzie powierzchnia z przedziału (−1 ; −0.5)

wredulus_pospolitus: kolejna sprawa −−−> gdybyś miała do wyznaczenia F(−0.5) i byś w taki sposób liczyła całkę, to by Ci wyszło: F(−0.5) = ∫^−0.5_0.5 f(t) dt co jest równe −∫^0.5_−0.5 f(t) dt = F(0.5) Więc by Ci wyszło F(−0.5) = −F(0.5) a że F(0.5) > 0 ... to co ... F(−0.5) < 0

ania: no ale zrobilam nie rozdzielajac na (−1;0) i (0:1) tylko (−1;1) stad roznica we wzorze mianowniku

wredulus_pospolitus: nie ma żadnej różnicy we wzorze

ania: no jak skoro potem sie sumuja przedzialy?

ania: a dobra

ania: chodzi ze przy 2 pomaranczowym ma byc w nawiasie kwadratowym −1/28 . . .

wredulus_pospolitus: zapis:

	⎧	0 gdy x ≤ −1
	⎜	a gdy x∊(−1;0)
F(x) =	⎨	a gdy x∊(0;1)
	⎩	0 gdy x≥1

zapis:

	⎧	0 gdy x ≤ −1
F(x) =	⎨	a gdy x∊(−1;1)
	⎩	0 gdy x≥1

zapis:

	⎧	0 gdy |x| ≥ 1
F(x) =	⎩	a gdy |x|<1

znaczą dokładnie to samo gdzie a = c(x²−5) z wyliczoną ją wartością 'c'

wredulus_pospolitus: przy 2 pomarańczowym Hęęęę

wredulus_pospolitus: w przedziale (−1;1) patrz na dolną granicę całki to jest błąd całkujesz od −1 czyli od końca poprzedniego przedziału

wredulus_pospolitus: a przy trzecim przedziale (1 ; +∞) trzecia całka górnej granicy NIE MA +∞ tylko x

ania: chodzi mi ze "drugim pomaranczowym" x( −1:1) ze w nawiasie kwadratowym jest zle zly mianownik

ania: bo ja musze zrobic w tym schemacie to zadanie https://ibb.co/Syz2qtS

ania: i jest problem z poprawnym zapisaniem tego

wredulus_pospolitus: bo ZAWSZE F(x) = ∫^x_−∞ f(t) dt <−−− powierzchnia pod funkcją gęstości od −∞ do x. A mając funkcję gęstości zapisaną w postaci klamerki możesz to rozdzielić na przedziały w ten sposób co robisz, ale nadal należy poprawne granice całkowania wstawiać winno być: 1. ∫^x_−∞ f(t) dt 2. ∫⁻¹_−∞ f(t) dt + ∫^x₋₁ f(t) dt 3. ∫⁻¹_−∞ f(t) dt + ∫¹₋₁ f(t) dt + ∫^x₁ f(t) dt

wredulus_pospolitus:

	3
c = −
	28

	⎧	0 gdy x ≤ 1
f(x) =	⎨	c(x3/3 − 5x) gdy x∊(−1;1)
	⎩	0 gdy x≥1

	3		15		3
natomiast: c(x2 − 5) = −		(x2 − 5) =		−		x2
	28		28		28

	15		3		15		1
a ∫		−		x2 dx =		x −		x3 zgadza się
	28		28		28		28

wredulus_pospolitus: w klamerce −−− oczywiście f(x) = c(x² − 5) gdy x∊(−1 ; 1)

ania: no ale mam ten zapis z 0:11 zapisac tak ze w pierwszej linicje wychodzi 0 w drugeij wzor a w 3 jeden?

ania: poza tym ja w klamerce potrzebuje dystrybuante

wredulus_pospolitus: 1. ∫_−∞^x 0 dt 2. ∫_−∞⁻¹ 0 dt + ∫₋₁^x 'a' dt 3. ∫_−∞⁻¹ 0 dt + ∫₋₁¹ 'a' dt + ∫₁^x 0 dt gdzie 'a' to te całe c(x² − 5) z wyznaczoną już wartością c. czyli liczysz cały przedział od −∞ do x. I w zależności gdzie ten 'x' się znajduje, dodajesz kolejne postacie funkcji gęstości. więc mamy policzyć (na przykład) F(0.5) to bierzemy cały przedział −∞ do −1 a w nim funkcja gęstości równa 0. + przedział od −1 do (w tym przypadku) 0.5, a w nim funkcja gęstości jest równa c(x²−5) a że podajesz 'w schemacie' ogólną postać (dla x a nie konkretnej wartości), to zamiast tego 0.5 wstawiasz 'x' w całce.

Ania: https://ibb.co/gdPFCRr

wredulus_pospolitus: Aniu ... klamerka to sposób zapisania funkcji (dowolnej funkcji ... w tym także funkcji gęstości − zresztą masz klamerkowo zapisaną gęstość w treści zadania).

wredulus_pospolitus: kiedy masz koło?

wredulus_pospolitus: teraz zapis jest

ania: ale co mam napisac 2 drugim przedziale i 3 po znakach rowna sie zeby w drugim wyszla fukcja jak w tym schemacie co wyslalam a w 3 jedynka

wredulus_pospolitus: tylko zapewne zamiast zapisywać f(t) dt w każdej całce ... postaw od razu postać funkcji gęstości z odpowiedniego przedziału.

ania: bo jak policze całke od −1 do x w drugim przedziale to nie wyjdzie mi wzór ogolny

ania: ale musze to zrobic w taki sposob zeby pierwsze bylo 0 potem wzor a potem 1 i potem zrobic klamerke i dopiero potem liczyc

wredulus_pospolitus: odnośnie pytania 00:31 −−−> patrz 00:28.

ania: widzialam ale nie rozumiem

ania: bo chodzi mi tylko o to jak zapisac tak to zdjecie dalej https://ibb.co/gdPFCRr zeby bylo jak tutuaj https://ibb.co/Syz2qtS

wredulus_pospolitus: jeszcze raz: 1. ∫_−∞^x 0 dt = 0

	3		15		t3
2. ∫−∞x 0 dt + ∫−1x −		t2 +		dt = 0 + [−		+
	28		28		28

	15
		t]x−1 =
	28

	x3		15		−1		15
= 0 + −		+		x − ( −		+		*(−1)) =
	28		28		28		28

	x3		15		1
= −		+		x −
	28		28		2

	3		15
3. ∫−∞x 0 dt + ∫−11 −		t2 +		dt + ∫1x 0 dt =
	28		28

	t3		15
= 0 + [−		+		t]1−1 + 0 =
	28		28

	1		15		−1		15		1		1
= −		+		− ( −		+		*(−1)) =		+		= 1
	28		28		28		28		2		2

sprawdź sobie na spokojnie podstawienia granic całkowania i zobacz, że się wszystko zgadza.

wredulus_pospolitus: błąd w podstawieniu w (2).

	x3		15
winno być −		+		x + 1/2 pogubiłem się z minusami
	28		28

wredulus_pospolitus: więc ... kiedy masz koło

ania: a w 2 w linijce nie powinno byc 15x/18

wredulus_pospolitus: ale skąd to 18 w mianowniku Ci wychodzi c(x²−5) <−−−− wyjściowa postać funkcji f(x) w przedziale (−1,1) tak Tak

	3
c = −		tak Tak
	28

PODSTAW

ania: w sensie t nie x

ania: le nie chodzi mi o 18 tylko 28 tylko chodzi mi czy tam nie ma byc razy t

ania: zle napisalam

ania:

	15		15
bo jest +		dt a nie		*t dt ?
	28		28

ania: a nie jest dobrze

wredulus_pospolitus: na przykładzie funkcji f(x) = x². gdy całkujemy ... i w GRANICY całki występuje 'x' to przecież nie możemy zapisać: ∫₁^x x² dx to nie ma sensu bo pod tym samym symbolem zapisujemy dwie różne rzeczy. dlatego używamy innego symbolu do zapisu 'zmiennej' w całce (tutaj akurat 't' ale to może być też 'y', 'z', czy 'chce mi się spać') i dlatego mamy ∫₁^x t² dt aby była jasność 'co jest czym' (i żeby nam się nie popierdzieliło)

	t3
natomiast podstawiając granice całkowania już w wyliczonej postaci [		]x1
	3

podstawiamy symbol 'x' w miejsce 't' (a także wartość '1' w miejsce 't'),

	x3		13		x3
więc będzie		−		=		− 1
	3		3		3

wredulus_pospolitus: to w końcu odpowiesz na pytanie −−−− kiedy masz koło

ania: koło znaczy kolokwium? Jakos za tydzien

wredulus_pospolitus: No to jeszcze trochę czasu masz. A jaki zakres na kole będzie tak −−− koło = kolokwium wydawało mi się, że to ponadczasowe określenie

ania: czyli ma byc F(X) = 0 dla (−∞ ; −1)

−x3		15x
	+		+ 0.5 , (−1;1)
28		18

1 dla x>1

ania: to i zmienna losowa ciagla jednostajna wykladnicza czy cos takirgo

wredulus_pospolitus: DOMYKAMY odpowiednio przedziały Bo Ci za to obetną punkty.

ania: kazdy przedzial ma byc domkniety?

wredulus_pospolitus: 'czy coś takiego' To nie ma tragedii. Ekonomia / zarządzanie Czy to (dziwnym trafem) wstęp do statystyki na jakiejś psychologii bądź innym społecznościowym kierunku

wredulus_pospolitus: Aniu −−−− dystrybuanta ma przedziały domknięte 'z której strony' na początku czy na końcu przedziału

ania: po prawej

ania: na koncu

wredulus_pospolitus: sprawdź w notatkach

ania: ze ma byc (−∞ ; −1> (−1; 1> i (1: ∞)?

wredulus_pospolitus: SPRAWDŹ W NOTATKACH

ania: Dystrybuanta F(x) ma przedziały domknięte z obu stron. Oznacza to, że do przedziału wlicza się zarówno jego lewą, jak i prawą granicę.

ania: (−∞ ; −1) <−1; 1> i (1: ∞)

wredulus_pospolitus: Wujek google Ci pomoże: https://www.statystyka-zadania.pl/dystrybuanta/ Nie wiem co Ty napisałaś ... mam szczerą nadzieję, że nie jest to coś co podał wykładowca, bo jeżeli tak to powinni go wypierdzielić z uczelni.

wredulus_pospolitus: W podstawowych własnościach dystrybuanty masz: FX(t) − prawostronnie ciągła, czyli jeżeli na wykresie wystąpi nieciągłość typu skok, to otwarta kropka będzie należeć do linii po lewej stronie, a zamalowana po prawej stronie Więcej o nieciągłości − kliknij <−−− kliknij tutaj

ania: czerwony link chyba nie dziala

wredulus_pospolitus: prawidłowy (bezpieczny) sposób zapisu przedziałów to będzie: (−∞,−1) ; <−1 ; 1) ; <−1 ; +∞) w naszym konkretnym zadaniu zapis który podałaś o 01:06 moglibyśmy 'obronić' ponieważ: lim_x−>1⁻ F(x) = F(1) = 1 .... ale bezpieczniej się trzymać tego co mówi definicja / własności, aby nie przejechać się przypadkiem.

wredulus_pospolitus: on nie jest czerwony ... masz pokreślone mniejszą czcionką (na tamtej stronie)

wredulus_pospolitus: tam kliknij nie w moim poście na czerwony zapis

ania: dziekuje

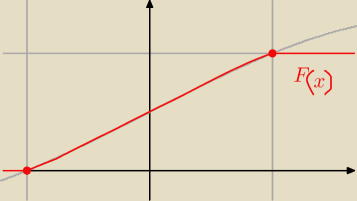
wredulus_pospolitus: w naszym zadaniu szczęśliwie dystrybuanta jest CIĄGŁA, więc jakbyś te przedziały domknęła (o ile byś je domknęła) to nie popełniła byś błędu ... ale to nie zawsze ma miejsce ... dlatego warto pamiętać którą stronę (bezpiecznie jest) domykać, a którą pozostawić otwartą.

wredulus_pospolitus: więc ... jaki kierunek studiujesz

ania: https://usosweb.uek.krakow.pl/kontroler.php?_action=katalog2/programy/pokazProgram&prg_kod=EI-AG-S1

.: Czyli kierunek społeczny. Zagadaj z ludźmi na forum, wydaje mi się że ktoś jest z miasta Kraka. Może poświęca Ci jakieś popołudnie na przerobienie zadań z Tobą w cztery oczy. Na pewno pójdzie szybciej i sprawniej niż na forum. Jakby co − tu wredulus, ale już z komórki pisze. A jeżeli nie − to wpadaj na forum z problemem, z pewnością ktoś Ci pomoże.