Czworokąt w okręgu www: Czworokąt o bokach: 3,4,5,6 wpisano w okrąg. Oblicz pole tego czworokąta.

chichi: skorzystaj ze wzoru Brahmagupty

www: Przepraszam, oblicz promień tego okręgu.

ABC: okrąg opisany na tym czworokącie jest jednocześnie okręgiem opisanym na matce wszystkich trójkątów prostokątnych 3,4,5

wredulus_pospolitus: ABC −−− pośpieszyłęś się z tą opinią ... gdyby to był ten sam okrąg, to znaczy że jego średnica jest równa 5, czyli mniejsza od najdłuższego boku.

Jolanta: Coś mi tu nie wychodzi Obliczam długość przekątnej czworokąta Mam dwa trójkąty Jeden o bokach,3,4 d i kacie α między bokami 3 i 4 drugi d,5,6 i kacie β między bokami 5 i 6 α+β=180⁰. β=180⁰−α d²=3²+4²−2*3*4cosα d²=5²+6²−2*5*6cosβ 9+16−24cosα=25+36−60cos(180⁰−α) 25−24cosα=25+36+60cosα −84cosα=36

	3
cosα=−
	7

	2		247
d2=25−24*(−3/7)=25+(72)/7=35		=
	7		7

d=√247/7

d
	=2R
sinα

Iryt: Podpowiedź: Jolu Skorzystaj : 1) z wzoru Brahmagupty 2) z tw. Ptolemeusza

	a*b*c
3 ) wzoru na pole Δ ( czterokrotnie): P=
	4R

reszta należy do Ciebie.

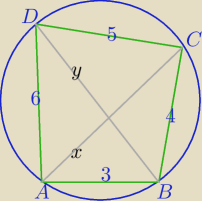
Iryt: AC=x, BD=y p=(3+4+5+6)/2=9 1) P_ABCD=P=√(9−3)*(9−4)*(9−5)*(9−6)=√30*12 P=√30*12 2) x*y=3*5+4*6, (*) xy=39 3)

	3*4*x		5*6*x
P={ΔABC}+PΔACD=		+		⇔
	2R		4R

	x*42
(**) P=
	4R

=========

	3*6y		4*5y
P=PΔABD+PΔBCD=		+
	4R		4R

	38y
(***) P=
	4R

4) z (*) , (**), (***)

	42*38xy
P2=
	16R2

	42*38xy
30*12=
	16R2

	42*38*39
30*12=
	16R2

R²=... dokończ

Jolanta: 1) i 2) Nic mi to nie mówi To jest w pełni gramie szkoły średniej?

Jolanta: W programie 🙂

Iryt: Rozszerzona matematyka.