krotki dowod z okregiem
krul: Dany jest okrag o srodku S oraz punkt D lezacy na tym okregu. Cieciwa AB przecina odcinek SD w
punkcie C roznym od S. Wykazac, ze AB > 2CD
6 kwi 14:13
wredulus_pospolitus:
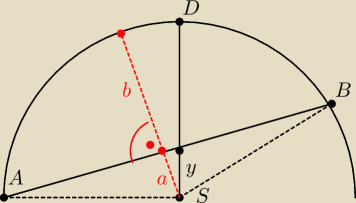 a
a +
b = r
wcześniej wykazałem, że |AB| > 2
b
a to odległość punktu S od odcinka (prostej) AB.
związku z tym |SC| = y
> a
a skoro |CD| + y = r = a + b −−> |CD|
< b
i stąd mamy:
|AB| > 2b > 2|CD|
c.n.w.
6 kwi 14:35
wredulus_pospolitus:
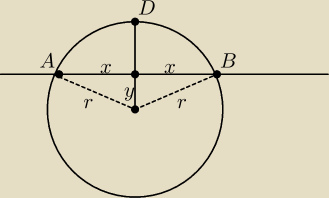 gdy AB ⊥ SD
gdy AB ⊥ SD
y = r − |CD|
| | |AB| | |
x2 = r2 − y2 = 2r|CD| + |CD|2 −−−> |
| = √2r|CD| + |CD|2 > √|CD|2 = |
| | 2 | |
|CD|
stąd: |AB| > 2|CD|
6 kwi 14:35
wredulus_pospolitus:
drugi post powinien być jako pierwszy

6 kwi 14:36
wredulus_pospolitus:
wykazanie a < y możemy też poprzez spojrzenie na trójkąt prostokątny który tworzą te dwa
odcinki i część odcinka AB.
y to długość przeciwprostokątnej ... więc musi zachodzić y > a
6 kwi 14:37
Eta:
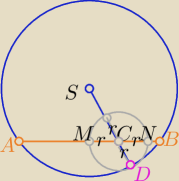
Kreśę mały okrąg o środku C i |CD|=r styczny wewnętrznie do dużego w punkcie D
to
|AB|>|MN|=2r=2|CD|
c.n.w.
6 kwi 19:35
 a + b = r
wcześniej wykazałem, że |AB| > 2b
a to odległość punktu S od odcinka (prostej) AB.
związku z tym |SC| = y > a
a skoro |CD| + y = r = a + b −−> |CD| < b
i stąd mamy:
|AB| > 2b > 2|CD|
c.n.w.
a + b = r
wcześniej wykazałem, że |AB| > 2b
a to odległość punktu S od odcinka (prostej) AB.
związku z tym |SC| = y > a
a skoro |CD| + y = r = a + b −−> |CD| < b
i stąd mamy:
|AB| > 2b > 2|CD|
c.n.w.
 gdy AB ⊥ SD
gdy AB ⊥ SD

 Kreśę mały okrąg o środku C i |CD|=r styczny wewnętrznie do dużego w punkcie D
to
|AB|>|MN|=2r=2|CD|
c.n.w.
Kreśę mały okrąg o środku C i |CD|=r styczny wewnętrznie do dużego w punkcie D
to
|AB|>|MN|=2r=2|CD|
c.n.w.