Punkt przecięcia
Little Mint:
Udowodnić że punkt przecięcia dwusiecznych dwóch kątów zewwnętrznych trójkąta leży na
dwusiecznej kąta wewnętrznego przy trzecim wierzchołku trójkąta
30 mar 23:04
wredulus_pospolitus:
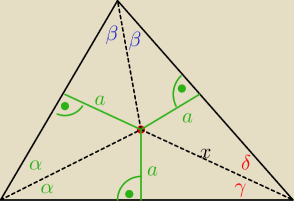
1. z podobieństwa trójkątów (bkk) o kącie 'α' mamy równość odległości tegoż punktu od dwóch
boków −> odległość równa 'a'
2. analogiczne podobieństwo dla trójkątów z kątem 'β' da nam równość dla trzeciej odległości.
| | a | |
3. z trygonometrii : sinγ = |
| = sinδ −−−> γ = δ lub γ = 180 − δ (niemożliwe do |
| | x | |
spełnienia w trójkącie)
PS. przy okazji 1 i 2 wykazuje, że punkt przecięcia się dwusiecznych wyznacza nam środek okręgu
wpisanego w tenże trójkąt, natomiast 'a' jest promieniem tegoż okręgu.
30 mar 23:19
Little Mint:
Dziękuje.
31 mar 00:46
wredulus_pospolitus:
Chciałbym wrócić do tego zadania −−− dopiero teraz przeczytałem, że tutaj chodzi o kąty
ZEWNĘTRZNE
3 kwi 10:20
chichi:
te równe odległości wynikają wprost z definicji dwusiecznej kąta, ktora mowi ze dwusieczna jest
to zbiór punktów równo odleglych od ramion kąta...
3 kwi 12:16
Iryt:
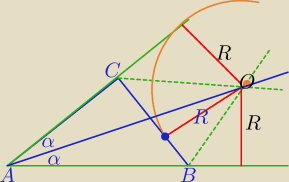
3 kwi 17:47