calka4 pedro: ₃ ∫ sgn(x−x³) dx ₀ wiem ze w sgn chodzi o znak i umiem liczyc calki na przedzialach ale calke z sgn to nie wiem

Min. Edukacji: Otwórz jakaś ksiqzke i poczytaj omtym

pedro: powiedzial co wiedzial

wredulus_pospolitus:

	⎧	1 jeżeli x(1−x2) > 0
sgn(x−x3) =	⎩	−1 jeżeli x(1−x2) < 0

związku z tym, że rozpatrujemy na przedziale [0;3] to mamy:

	⎧	1 gdy x∊ (0;1)
sgn(x−x3) =	⎩	−1 gdy x ∊ (1;3)

związku z tym ∫₀³ sgn(x−x³) dx = 1*1 + 2*(−1) = −1

pedro: a skąd to że 1 lub −1?

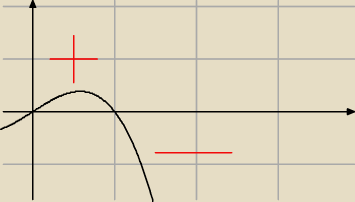
wredulus_pospolitus: ze względu na wykres g(x) = x − x³ wiemy, jaką wartość f(x) = sgn(x−x³) przyjmuje w danym przedziale

pedro: a bo to chodzi o znak

pedro: zapomnialem

pedro: a moglbys rozjasnic ten zapis związku z tym ∫03 sgn(x−x3) dx = 1*1 + 2*(−1) = −1

pedro: bo nie bardzo wiem skad sie to wzielo

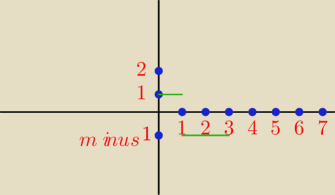
.: A narysuj sobie f(x) = sgn(x−x³) na przedziale [0,3] skoro już Ci narysowałem g(x) = x−x³ na tymże przedziale.

pedro:

wredulus_pospolitus: nom ... i teraz masz obszar od x=0 do x=1 o wartości 1 ... więc wartość całki to będzie długość * wartość = 1*1 = 1 i masz obszar od x=1 do 3 o wartości −1 ... więc wartość całki to będzie długość * wartość = 2 * (−1) = −2 dodajesz wartości całki z tych obszarów i masz wartość całki od x = 0 do x = 3

Pedro: Ale właściwie czemu długość razy wartość? Trochę nie rozumiem tego liczenia tutaj całki w takim dziwnym przypadku

wredulus_pospolitus: Interpretacja GEOMETRYCZNA całki oznaczonej: Wartość całki z f(x) na przedziale (a,b) jest równa sumarycznej powierzchni pomiędzy krzywą f(x) a osią OX gdy f(x) > 0 ODJĄĆ sumaryczna powierzchnia pomiędzy krzywą f(x) a osią OX. Z tego też powodu na przykład: ∫₀^2π sinx dx = 0 (powierzchnia 'powyżej osi OX' = powierzchnia 'poniżej osi OX'). A w naszym przypadku będzie to powierzchnia powyżej osi OX (1*1 = 1) − powierzchnia poniżej osi OX (1*2 = 2) co daje nam 1 − 2 = −1

wredulus_pospolitus: o ile w przypadku funkcji g(x) = sinx (czy nawet h(x) = x − x³) ciężko by było nam policzyć powierzchnię pomiędzy krzywą a osią OX inną metodą jak całka (bądź metody numeryczne), o tyle w przypadku funkcji sgn( f(x) ) jest to bardzo proste ze względu na to, że te powierzchnie są po prostu prostokątami. Związku z tym łatwiej nam w taki sposób rozwiązać tą całkę (pokazując jednocześnie, że rozumiemy co właściwie liczymy licząc całkę oznaczoną) niż kombinować jak zapisać funkcję pierwotną.

Pedro: Tak to że odjąć rozumiem ale zastanawia mnie czemu nie liczymy jak zawsze Tzn jak jest na przedziale (0:1) równa y=1 to po prostu ∫1 = x + c I analogicznie z tym −1

wredulus_pospolitus: Chcesz ... licz sobie tak ... wyjdzie dokładnie to samo. Nie wiem co studiujesz, więc nie wiem jakie będziesz miał zajęcia. Ja do dziś pamiętam jak na studiach miałem liczyć siły które oddziaływują na belkę. Mieliśmy siły osiowe, siły ścinające i momenty zginające (przykład jakbyś był ciekaw: https://www.youtube.com/watch?app=desktop&v=A4kAA3Lu_Q8). Na filmiku możesz zobaczyć, że najwięcej 'poci' się człowiek z momentem zginającym. Ludzie w mojej grupie byli uczeni tak samo i każdy robił w ten sposób. Ja (początkowo) jako jedyny korzystałem z faktu, że wartość momentu obrotowego w danym punkcie będzie równa całce oznaczonej z sił ścinających (nie do końca ... czasami poprawkę dajemy na momenty zaznaczone na belce, ale to była rzadkość) przemnożony przez −1, a wykres momentu będzie odpowiadał całce nieoznaczonej. Jako, że belki były proste (mieliśmy siłę punktową kub równomiernie rozłożoną), to wykresem siły tnącej (na danym odcinku) była albo funkcja stała albo funkcja liniowa, więc prozaicznie szybko liczyło się pole powierzchni (całka oznaczona) jak również wykres momentu to była albo funkcja liniowa albo fragment paraboli (całka nieoznaczona). Do czego zmierzam −−− Pięknem matematyki jest to, że w wielu przypadkach masz parę dróg do celu i tylko od Ciebie zależy którą z nich wybierzesz. Jedna będzie (w Twoim odczuciu) łatwiejsza niż inna.

pedro: dzieki wielkie

wredulus_pospolitus: taka uwaga do tego co napisałem o belkach −−− ja oczywiście nie liczyłem całek tylko liczyłem pole prostokąta bądź trójkąta, czyli korzystałem z interpretacji geometrycznej całki oznaczonej (bo tak było szybciej).