W czworościan foremny o krawędzi 12 wpisano kulę.
Bezimienny: W czworościan foremny o krawędzi 12 wpisano kulę. Czworościan ten przecięto płaszczyzną
styczną do wpisanej kuli dzielącą czworościan na ostrosłup oraz ostrosłup ścięty. Oblicz
objętość powstałego ostrosłupa.
Poprawna odpowiedź to 18
√2, ale średnio wiem, jak do niej dotrzeć
28 mar 18:05
wredulus_pospolitus:
masz rysunek
28 mar 20:33
Eta:
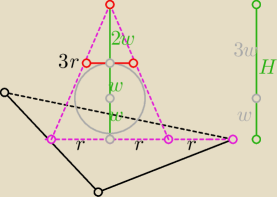
ostrosłup(mały) odcięty jest podobny do ostrosłupa (dużego) w skali k= 4w/2w= 2
| | 1 | |
w= |
| H −− dł. promienia kuli wpisanej |
| | 4 | |
Vd= 144
√2
Vm= 8
√2
=========
28 mar 20:40
Eta:
Poprawiam zapis
Vm= 18√2
28 mar 20:42
wredulus_pospolitus:
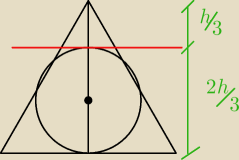
z podobieństwa figur:
| | 1 | | 1 | | 123 √2 | |
Vmałego ostrosłupa = ( |
| )3Vwyjściowego ostrosłupa = |
| * |
| = |
| | 3 | | 33 | | 12 | |
| | 122√2 | | 16√2 | |
= |
| = |
| i taka odpowiedź powinna Ci wyjść |
| | 33 | | 3 | |
28 mar 20:44
Eta:
Echhh jeszcze poprawiam
.............................................. w skali k= 2w/4w=1/2
28 mar 20:44
Eta:
I co
wredulusie ?
28 mar 20:51
wredulus_pospolitus:
fakt ... źle 'ciąłem' czworościan
28 mar 20:53
Eta:
A może "podcięty" jesteś ?
28 mar 20:53