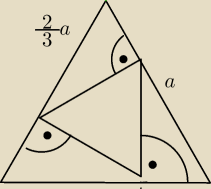
Szerego Michal: Dany jest trójkąt równoboczny T1 o boku a. W ten trójkąt wpisujemy trójkąt równoboczny T2 tak, że każdy wierzchołek trójkąta T2 należy do innego boku trójkąta T1 i kąt ostry α między bokami trójkątów T1 i T2 wynosi 30◦. W ten trójkąt wpisujemy analogicznie trójkąt T3, itd. .Ile wynosi suma nieskończonego ciągu pól wszystkich utworzonych w ten sposób trójkątów?

mam pytanie: S=a+2/3a+4/9a+8/27a+...

	a
S=		=3a
	1−2/3

mam pytanie: oj pomyłka S=a+a√3/3+a/2+a√3/4 +3/8a+... a₁=a q=√3/2

	a		a		2a		2+√3
s=		=		=		*		=2a(2+√3)
	1−√3{2}		(2−√3)/2		2−√3		2+√3

mati:

	√3
q=
	3

kerajs:

	a2√3		a2√3		3
S=		(1+q2+(q2)2+(q2)3+....)=		*
	4		4		2