Geometria analityczna Adam: W okrąg o równaniu (x + 2)² + (y − 4)² = 25 wpisano trójkąt ABC , którego pole jest równe 20. Bok AB tego trójkąta jest zawarty w prostej o równaniu 4y+ 3x − 10 = 0 , a wysokość opuszczona z wierzchołka C przecina bok AB w punkcie D , którego obie współrzędne są dodatnie. Oblicz współrzędne punktu D .

chichi: wyznaczamy z układu natychmiastowo wierzchołki A = (−6,7) oraz B = (2,1), ponadto zauważamy, że środek S = (−2,4) okręgu leży na prostej 4y + 3x − 10 = 0, a to oznacza, że AB jest średnicą okręgu, a zatem ΔABC jest prostokątny, dasz radę dalej? jeśli nie to pisz

Adam: Doszedłem do tego momentu i tutaj jest problem, bo mam, że ten trójkąt jest prostokątny obliczyłem, spodek wysokości h= 4, ale nie wiem co dalej.

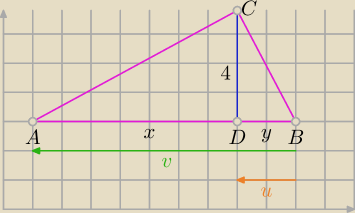
chichi: mamy: 4² = xy ∧ x + y = 10 ⇔ (x,y) ∊ {(2,8), (8,2)}, jedynie para liczb (x,y) = (8,2) spełnia warunki zadania o dodatniości współrzędnych punktu D, więc tylko tę parę pokażę.

	1
v = vec(BA) = [−8,6], u = vec(BD) = [xD − 2, yD − 1], ponadto u =		v, stąd
	5

	1		2		11
[xD − 2, yD − 1] =		[−8,6] ⇔ xD =		∧ yD =
	5		5		5

Adam: A da się inaczej niż wektorami?