Walec wpisany w stożek, optymalizacja Piotrekkk: Spośród wszystkich walców wpisanych w stożek, którego przekrój osiowy jest trójkątem równobocznym o boku 2a, wybrano ten o największej objętości. Wykaż, że objętość tego walca jest równa objętości kuli wpisanej w dany stożek. Nie mam pojęcia jak to zrobić.

wredulus_pospolitus: oblicz objętość tegoż walca ... oblicz objętość kuli ... i porównaj

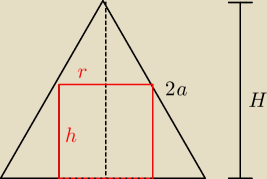
wredulus_pospolitus: z podobieństwa trójkątów:

r		a
	=
H−h		H

w ten sposób masz zależność pomiędzy 'r' a 'h' walca. Wstawiasz do wzoru na objętość ... szukasz minimum (wierzchołek paraboli lub z pochodnej).

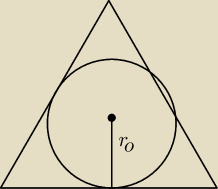
wredulus_pospolitus: r_o = masz tutaj okrąg wpisany w trójkąt równoboczny wzór na objętość kuli o promieniu r_o porównujesz i gotowe

Piotrekkk: Wielkie dzięki.